At what rate of deceleration will the liquid level of the figure below just reach the top of the tank ?

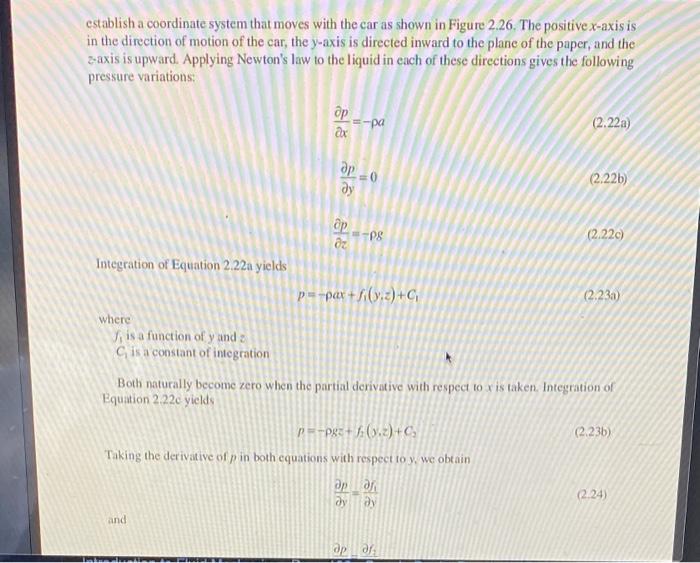
In the problems we have discussed thus far, forces due to pressure variations were simple to compute because the fluid was at rest and hence, there were no shear stresses between adjacent layers of fluid. A liquid transported at a uniform rate of aceeleration is also motionless with respect to its container. Consequently, there are no shear stresses, and here too forces due to pressure variations are simple to calculate. Uniformly rotating fluids represent another case of interest. When a liquid is rotating at a constant angular velocity, it is acted upon by centripetal accelemtion forces Because the liquid is at rest with respect to its container, forees due to pressure variations are again simple to calculate. To illustrate this phenomenon, consider the setup shown in Figure 2.26. A rectangular transparent box is attached to a model railroad flatear that is free to traverse a track. A rope tied to the car is: wrapped over a pulley and attached to a weight. As the weight falls, the car accelerates at a. Next we establish a coordinate system that moves with the car as shown in Figure 2.26. The positive x-axis is in the direction of motion of the car, the y-axis is directed inward to the plane of the paper, and the zaxis is upward. Applying Newton's law to the liquid in each of these directions gives the following pressure variations: xp=a (2.22a) yp=0 Integration of Equation 2.22 a yields zp=g p=ax+f1(y,z)+C1 where f1 is a function of y and C1 is a constant of integration Both naturally become zero when the partial derivative with respect to x is taken. Integration of Equation 2.22c yields p=gz+f2(y,z)+C2 Taking the derivative of p in both equations with respect to y, we obtain yp=yfi (2.24) and R=pRt+f(y,c)+C1 Taking the derivative of p in both equations whi respect b y we obtain dy22=2y2 and yy=2tf Inspection of Equatien 222b leads to the coecluica that noither f,norf, is a function of y, Equating Equalions 2.23a and hwe get pax+fA(z)+C1=pt2+f1(x)+C1 which icads to f1(t)=pt2f2(x)=pkrxC1=C3 Ther clove, the preswure in Equation 2.23 becomet plopiurht+Ci Hud Statick p1=p2+ti ci=perpet The pre wuse is then pp;=p[g(zz)ax] (x(x4)=x