Attached below are microeconomic questions, try and provide answers for them
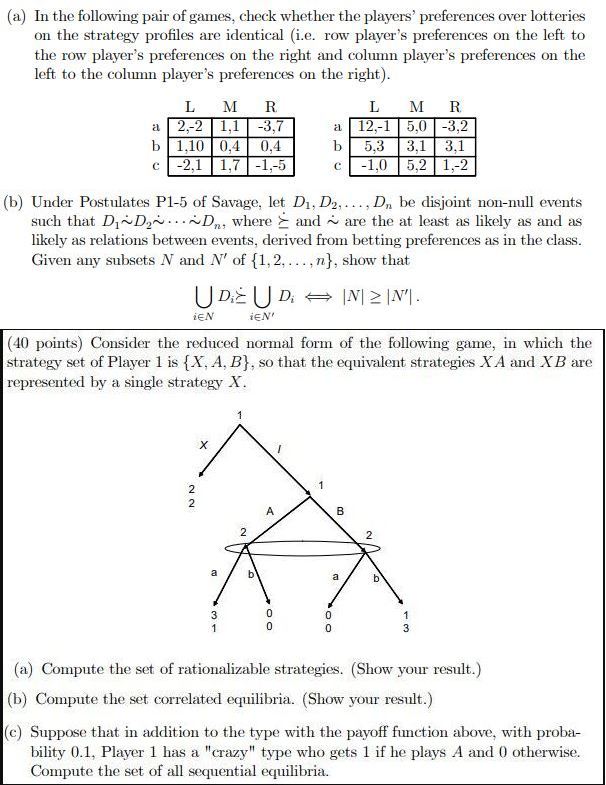
(a) In the following pair of games, check whether the players' preferences over lotteries on the strategy profiles are identical (i.e. row player's preferences on the left to the row player's preferences on the right and column player's preferences on the left to the column player's preferences on the right). L M R L M R 2.-2 1,1 -3,7 12.-1 5.0 -3,2 1,10 0,4 0,4 5.3 3,1 3.1 -2,1 1,7 -1,-5 -1,0 5.2 1,-2 (b) Under Postulates P1-5 of Savage, let D1, D2. .... D, be disjoint non-null events such that Di~Dy...~Dn, where > and ~ are the at least as likely as and as likely as relations between events, derived from betting preferences as in the class. Given any subsets N and N' of {1, 2. ....n}, show that UD UD - IN1 2 IN'. iEN iEN' (40 points) Consider the reduced normal form of the following game, in which the strategy set of Player 1 is {X, A, B}, so that the equivalent strategies X A and X B are represented by a single strategy X. X NO N 2 (a) Compute the set of rationalizable strategies. (Show your result.) (b) Compute the set correlated equilibria. (Show your result.) (c) Suppose that in addition to the type with the payoff function above, with proba- bility 0.1, Player 1 has a "crazy" type who gets 1 if he plays A and 0 otherwise. Compute the set of all sequential equilibria.An economy has two agents, Bill and Bob. Bill has $110, and Bob has $200. Utility of agents in this economy is characterized by the following function of income: U = u(y) = [ log(y - 60) if y 160 The minimum level of income possible in this economy is 60. Each agent is about to choose a new business venture, and has a choice between project A and project B. Neither project requires any investment up front. Project A yields revenues of 20 with probability = and revenues of -10 with probability -. Project B yields revenues of 4 with probability one-half and revenues of 5 with probability one-half. Throughout this problem, assume that fractional income is possible. (a) (5 points) Which project would each agent choose? Provide intuition for your answer. (b) (5 points ) If Bill and Bob each choose an investment project each year and receive the associated income for 20 years, will the expected gap in their incomes be larger or smaller at the end of this period than it was initially ? How does this relate to attitudes toward risk? You do not need to calculate income over 20 years, just provide intuition. (c) (10 points) Now, assume that there is a job available that provides fixed wage income. What salary would the job have to provide in order to induce Bill to take the job rather than entering a new business venture? What salary would the job have to provide in order to induce Bob to take the job? Which is higher, and why? Algebraic expressions are acceptable as answers.Alice has A dollars and has a constant absolute risk aversion a (i.e. u (r) = =e "?) for some a > 0. With some probability # 6 (0, 1) she may get sick, in which case she would need to spend L dollars on her health. There is a health-insurance policy that fully covers her health care expenses in case of sickness and costs P to her. (If she buys the policy, she needs to pay P regardless of whether she gets sick.) (a) Find the set of prices P that she is willing to pay for the policy. How does the maximum price P she is willing to pay varies with the parameters M. L. o, and a? (b) Suppose now that there is a test te {-1, + 1} that she can take before she makes her decision on buying the insurance policy. If she takes the test and the test t is positive, her posterior probability of getting sick jumps to * * > * and if the test is negative, then her posterior probability of getting sick becomes 0. What is the maximum price c she is willing to pay in order to take the test? Take P " (E) >0 > > > u (D). Find the condition under which she takes the test. (b) (4 minutes) Calculate consumer and producer surplus under trade. (5) (15 minutes) The US government is unhappy with steel imports and decides to impose a 200 percent tariff on imported steel so that the price of imported steel is now 3 when importing from abroad. (Continue to assume that the US domestic steel market operates in perfect competition with production function S(L) = ;1) (a) (2 minutes) What is the price of domestic steel? Will car manufacturers choose to use domestic or foreign steel? (b) (5 minutes) Calculate the new equilibrium in the US market for cars, continuing to assume that cars are traded freely at a world price of 100. Does the US still export cars