Dividing polynomials. The degree of a polynomial is the exponent on the highest power of x. For example,

has degree 10, and the degree of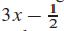 

is 1. When the polynomial is just a number (there are no x terms), we say the degree is 0. The polynomial 0 is exceptional; we say its degree is -∞. If p is a polynomial, we write deg p to stand for its degree. You may assume that the coefficients of the polynomials we consider in this problem are rational numbers.

a. Suppose p and q are polynomials. Write a careful definition of what it means for p to divide q (i.e., p|q).

Please verify that    is true in your definition.

b. Give an example of two polynomials p and q with p ≠ q but p|q and q|p.

c. What is the relationship between polynomials that divide each other?

d. Prove the following analogue of Theorem 35.1:

Let a and b be polynomials, with b nonzero. Then there exist polynomials q and r so that a = qb + r with deg r < deg b.

 

e. In this generalized version of Theorem 35.1, are the polynomials q and r uniquely determined by a and b?

Theorem 35.1:  

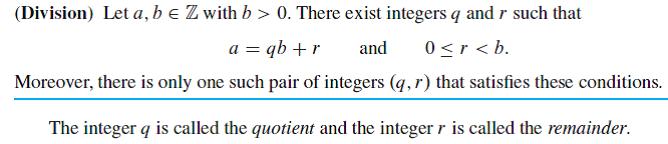
x10 - 5x2 + 6