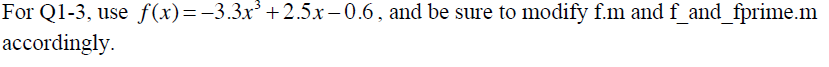
% Bisection.m Lines of code 17-26 and 43-47 are bold

% This code finds the root of a function f(x) in the interval [a, b] using the Bisection method

%

% It uses f.m to define f(x), and assumes f(x) is continuous

% It requires specification of a, b and the maximum error

% It defines error using |f(xnew)|

% Define inputs for problem

a=0; %Defines lower limit of initial bracketing interval

b=1; %Defines upper limit of initial bracketing interval

errmax = 1E-4; %Defines maximum error

%Get function values associated with initial interval endpoints

fa = f(a); %get function value at a

fb = f(b); %get function value at b

% Let MATLAB figure out which end point is "plus" and which is "minus"

if fa>0 & fb

xplus = a;

xminus = b;

elseif fa 0

xplus = b;

xminus = a;

else

'Not a valid bracketing interval'

return

end

iter = 0; %Initialize iteration counter (not required, but for interest)

err = 1; %Initial value of err is set large to ensure enter loop.

while err > errmax %Iteration loop

%Increase iteration counter

iter=iter+1;

%Get xnew using Bisection

xnew = (xplus + xminus)/2;

%Get f(xnew)

fnew = f(xnew);

%Adjust bracketing interval based on sign of f(xnew)

if fnew > 0

xplus = xnew;

else

xminus = xnew;

end

err = abs(fnew); %This is the error metric for this example.

end

'Root is'

xnew

iter

......................................................................................NEW CODE...............................................................

%Textbooks bisect.m lines of code 19 24 are Bold

function bisect(f,a,b,tol,n)

% Bisection method for solving the nonlinear

%equation f(x)=0.

a0=a;

b0=b;

iter=0;

u=feval(f,a);

v=feval(f,b);

c=(a+b)*0.5;

err=abs(b-a)*0.5;

disp('_____________________________________________________________________')

disp(' iter a b c f(c) |b-a|/2 ')

disp('_____________________________________________________________________')

fprintf(' ')

if (u*v

while (err>tol)&(iter

w=feval(f,c);

fprintf('%2.0f %10.4f %10.4f %12.6f %10.6f %10.6f ',iter,a,b,c,w,err)

if (w*u

b=c;v=w;

end

if (w*u>0)

a=c;u=w;

end

iter=iter+1;

c=(a+b)*0.5;

err=abs(b-a)*0.5;

end

if (iter>n)

disp(' Method failed to converge')

end

else

disp(' The method cannot be applied f(a)f(b)>0')

end

% Plot f(x) in the interval [a,b].

fplot(f, [a0 b0])

xlabel('x');ylabel('f(x)');

grid

For 01-3, use f (x)E-3.3x3 +2.5x -0.6, and be sure to modify f m and f and fprime.m accordingly