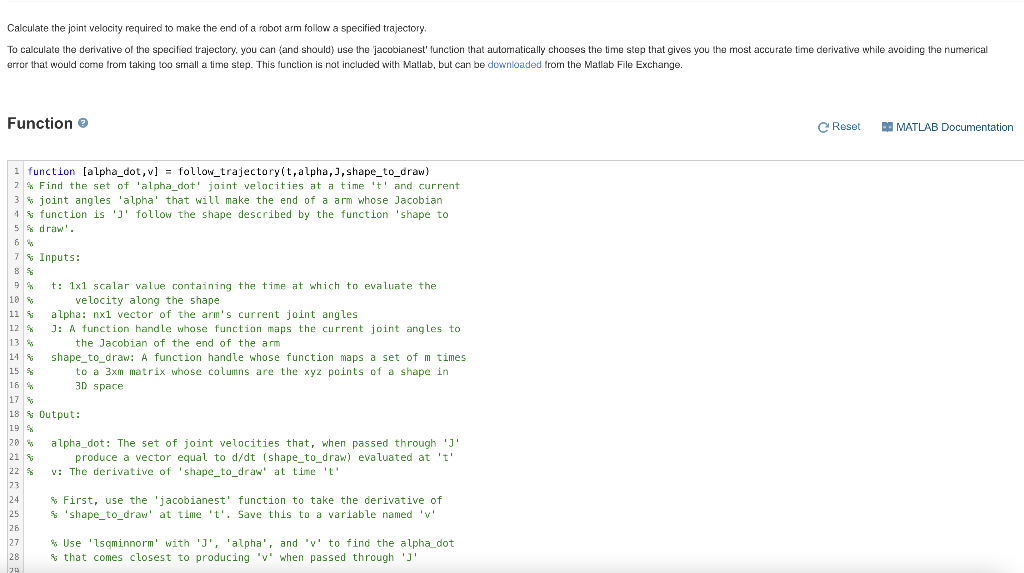
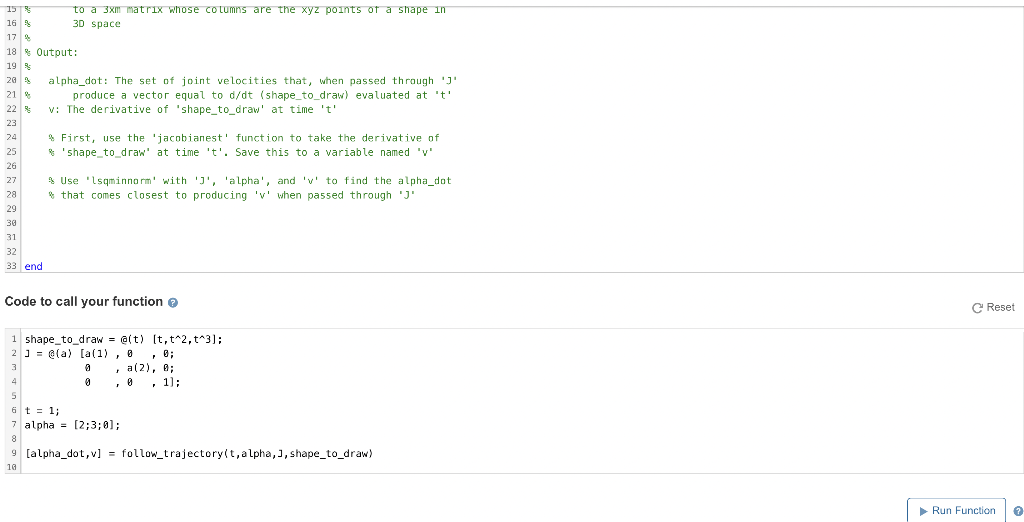
Calculate the joint velocity required to make the end of a robot arm follow a specified trajectory, To calculate the derivative of the specified trajectory, you can (and should use the 'jacobianest' function that automatically chooses the time step that gives you the most accurate time derivative while avoiding the numerical error that would come from taking too small a time step. This function is not included with Matlab, but can be downloaded from the Matlab File Exchange. Function e Reset - MATLAB Documentation i function (alpha_dot, v] = follow_trajectory(t,alpha,2, shape_to_draw) 2 * Find the set of 'alpha_dot' joint velocities at a time 't' and current 3 joint angles 'alpha' that will make the end of a arm whose Jacobian 1 $ function is 'l' follow the shape described by the function 'shape to 5 draw'. 6% 7 Inputs: 99 t: 1x1 scalar value containing the time at which to evaluate the 10 velocity along the shape 11 % alpha: nxi vector of the arm's current joint angles 12 S J: A function handle whose function maps the current joint angles to 13 the Jacobian of the end of the arm 14 4 shape_to_draw: A function handle whose function maps a set of m times 15 5 to a 3xm matrix whose columns are the xyz points of a shape in 16 % 3D space 17 18 Output: 19 6 20 % alpha_dot: The set of joint velocities that, when passed through 'J' 21 S produce a vector equal to d/dt (shape_to_draw) evaluated at 't' 22 v: The derivative of 'shape_to_draw' at time it' 23 24 First, use the 'jacobianest' function to take the derivative of 25 $ 'shape_to_draw' at time 't'. Save this to a variable named 'v' 25 * Use 'lsaminnorm' with 'J', 'alpha', and 'v' to find the alpha_dot 28 that comes closest to producing 'v' when passed through 'l' 20 27 15 to a 3x matrix whose columns are the xyz points of a shape in 16 B 3D space 17 9 18 Output: 19 20 alpha_dot: The set of joint velocities that, when passed through 'l' + 21 produce a vector equal to d/dt (shape_to_draw) evaluated at 22 V: The derivative of 'shape_to_draw' at time 't' 23 24 % First, use the 'jacobianest' function to take the derivative of 25 & 'shape_to_draw' at time 't'. Save this to a variable named 'v' 26 27 Use 'lsqminnorm' with 'I', 'alpha', and 'v' to find the alpha_dot that comes closest to producing 'v' when passed through 'J 28 29 30 31 32 33 end Code to call your function C Reset P 1 shape_to_draw = @t) [t,t^2,t^3]; 2 ] = (a) [a(1), ; ] @ 5 3 a ,a(2), 8; 4 0 0 , , 1); 5 6 t = 1; 7 alpha = [2;3;0]; 8 9 [alpha_dot, v] = follow_trajectoryit, alpha,, shape_to_draw) 19 Run Function