Calculus 1 Please help me answers and explanations

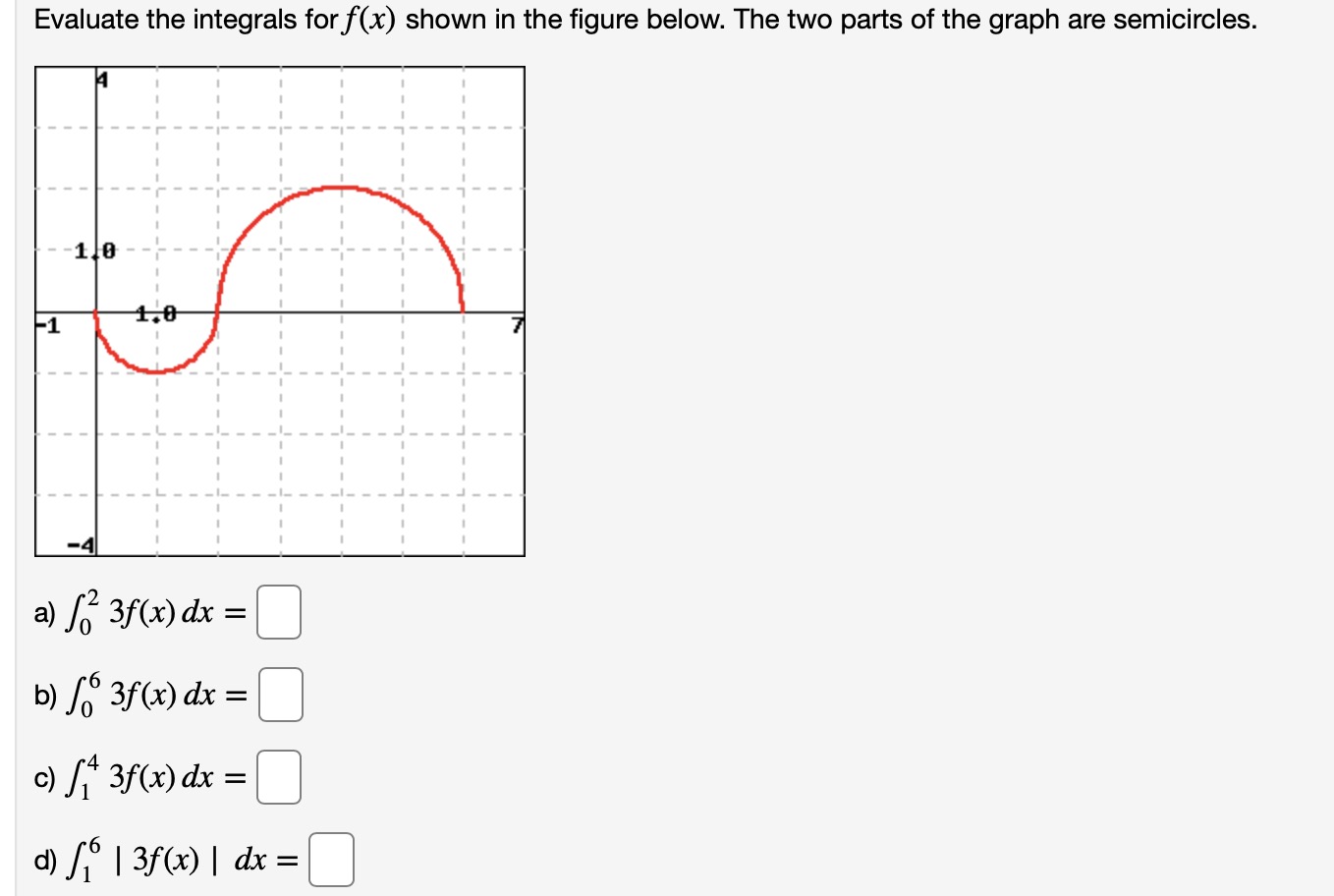
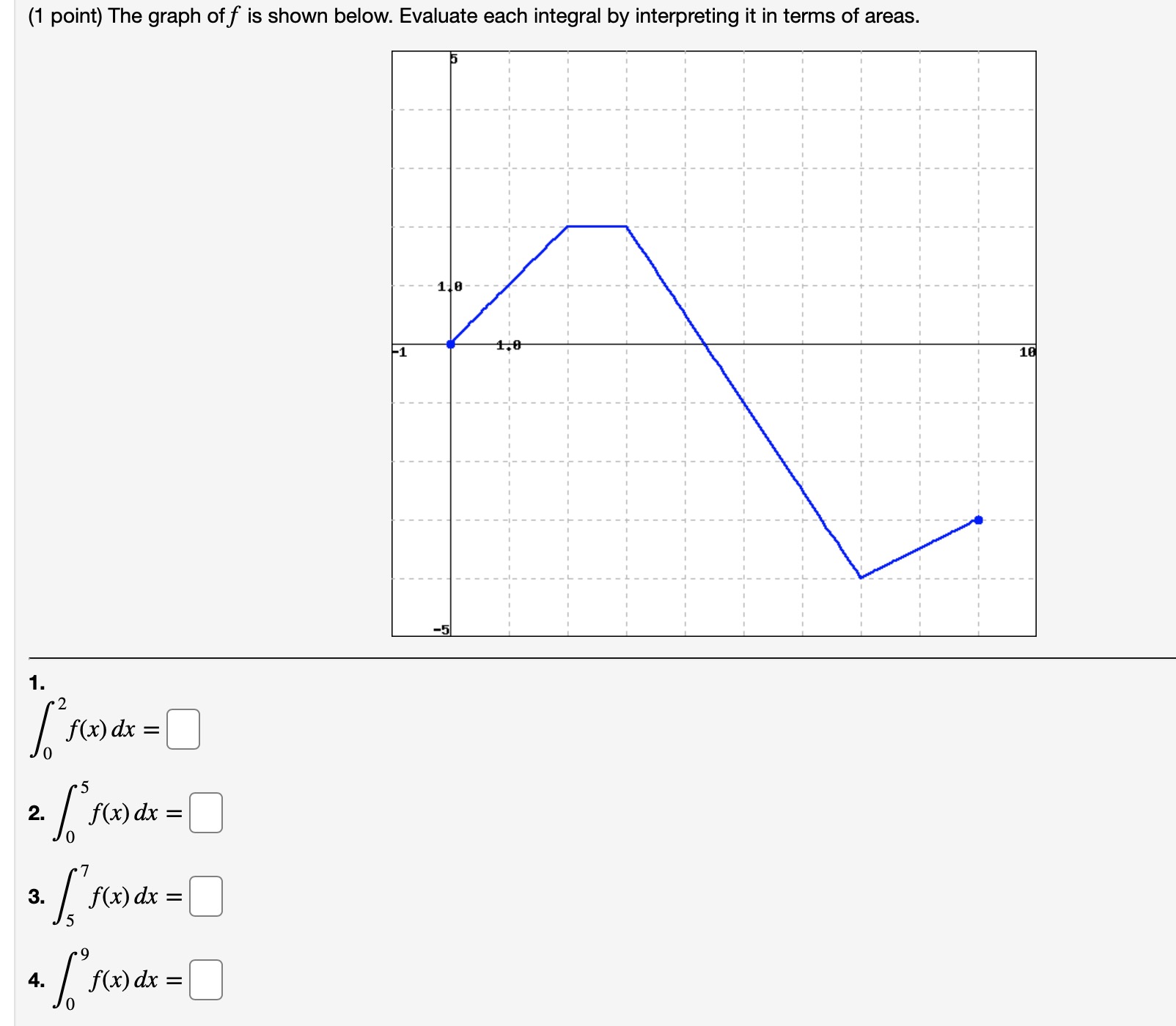
(1 point) Suppose Evaluate the definite integral by interpreting it in terms of signed area. fogf(x)dx=C] Suggestion: Draw a picture of the region whose signed area is represented by the integral. Then find the signed area using formulas from high school geometry. \fCompute the indicated integral by findng the area of the trapezoidal figure below. \f(1 point) In each part, find a formula for the general term of the sequence, starting with n = 1. Enter the following information for an =. (a) L L L 4 16' 64' 256' 1024"" an=Cl (b) L _; L _ 1 16' 64'256' 1024"" an = (C) 1 g Q a 4' 16'64' 256"" an = (d) 0, 1 Consider the sum. H k3 24 k=1n Write a formula to compute the sum for any natural number n. Answer:C] Compute the limit. n 3 9mg=C1 Suppose 2 f(x) = x_ 12' (a) The rectangles in the graph on the left illustrate a left endpoint Riemann sum for f(x) on the interval 3 5 x 5 5. The value of this left endpoint Riemann sum is C] , and it is an ? the area of the region enclosed by y = f(x), the x-axis, and the vertical lines 36 = 3 and x = 5. (b) The rectangles in the graph on the right illustrate a right endpoint Riemann sum for f(x) on the interval 3 5 x S 5. The value of this right endpoint Riemann sum is C] , and it is an ? the area of the region enclosed by y = f(x), the x-axis, and the vertical lines )6 = 3 and x = 5. Suppose f(x) = E- x (a) The rectangles in the graph on the left illustrate a left endpoint Riemann sum for f(x) on the interval 2 S x 5 4. The value of this left endpoint Riemann sum is C] , and it is an ? the area of the region enclosed by y = f(x), the x-axis, and the vertical lines x = 2 and x = 4. (b) The rectangles in the graph on the right illustrate a right endpoint Riemann sum for f(x) on the interval 2 S x 5 4. The value of this right endpoint Riemann sum is C], and it is an ? the area of the region enclosed by y = f(x), the x-axis, and the vertical lines x = 2 and x = 4. Evaluate the integrals for f(x) shown in the figure below. The two parts of the graph are semicircles. -110 -1 1.0 a ) 12 3f ( x ) dx = b) So 3f ( x) dx = c) S 3f (x) dx = d ) 6 13f ( x ) 1 dx =(1 point) The graph of f is shown below. Evaluate each integral by interpreting it in terms of areas. -110 140 16 1 . 2. ( f(x)dx = 3. ( f()dx = ] 1. f(x) dx = 0(1 point) Suppose 4 ifzgx