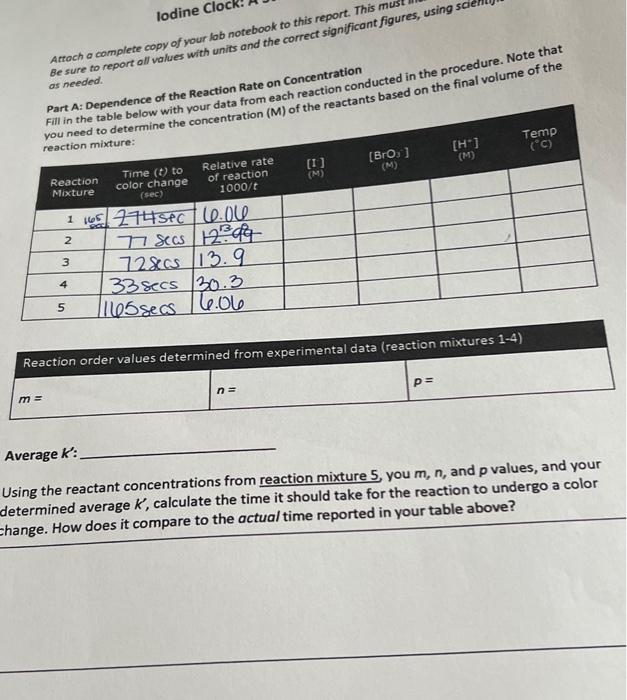
can you help me with the processing the data part with the time given in the table

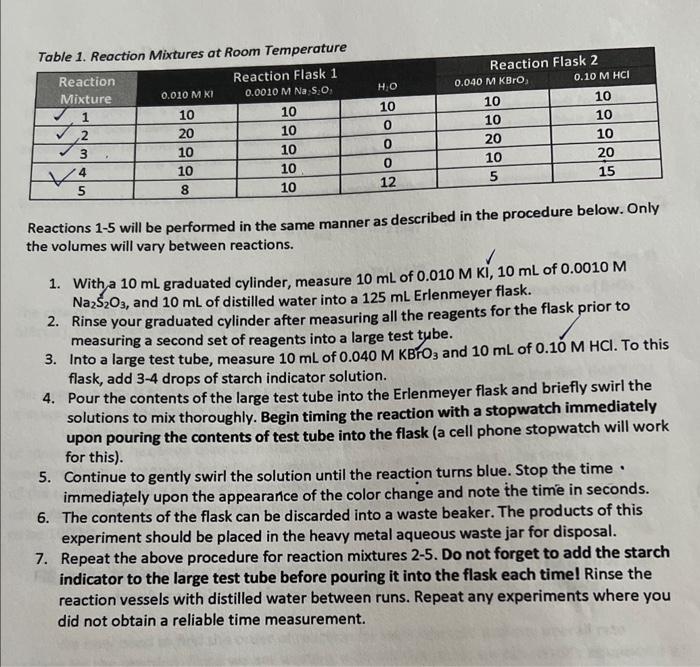
Experiment 4A - lodine Clock: A Study of Reaction Rates Overview The rate at which a chemical reaction proceeds depends on several factors: the nature of the reaction, the concentrations of the reactants, the temperature, and the presence of possible catalysts. For a given reaction, the rate typically increases with an increase in the concentration of any reactant. The relation between rate and concentration is a simple one, in most cases. As an example, consider the reaction: aA+bBcC The rate of this reaction can usually be expressed by the equation: Rate=k[A]m[B]n (Eqn 1) where m and n are usually (but not always) integers, specifically with values of 0,1,2, and rarely 3. The concentrations of A and B (in moles per liter, M ) are represented as [A] and [B], and k is a constant, called the rate constant of the reaction, which makes the reaction quantitatively correct. The numbers m and n are called the orders of the reaction with respect to A and B. If m is 1 , the reaction is said to be first order with respect to the reactant A. If n is 2 , the reaction is second order with respect to reactant B. The overall order is the sum of m and n. In this example, the reaction would be third order overall. In this experiment, we will study the kinetics of a reaction that is part of a family of reactions commonly called an "iodine clock." These reactions are so named because when combined with a starch indicator, the colorless iodide ion becomes triiodide in the course of the reaction, and combines with the starch producing a sudden, intense color change to dark blue. This color is visible to the naked eye when the concentration of triiodide ion exceeds 105M. The reaction that we will be studying is as follows: 6I(aq)+BrO3+6H(aq)+3I2(aq)+Br(aq)+3H2O(q)(Eqn2) The rate law of this reaction can therefore be expressed as: Rate=k[I]m[BrO3]n[H+]p where m,n, and p are the orders of the reaction with respect to iodide, bromate, and hydrogen ion, and k is the rate constant of the reaction. To obtain a time delay with a sharp color change, we introduce a "clock" into the reaction in the form of a reducing agent, thiosulfate. This reaction is as follows: I2(aq)+2S2O3(aq)22I(aq)+S4O6(aq)2 Relative to reaction 3 , this reaction is practically instantaneous. The molecular iodine produced in reaction 3 reacts completely with the thiosulfate ion, S2O32, so that until all the thiosulfate ion has reacted completely, the concentration of iodine remains effectively zero. As soon as the thiosulfate ion is consumed, the iodine produced by 3 begins to accumulate in the solution. The presence of iodine becomes immediately apparent because even small concentration of lodine causes the indicator to turn a deep blue color. The "clock" tells us when a given amount of BrO;' ion has reacted ( 1/6 mole of BrOs' per mole of S2O322 ). Importantly, the rate of reaction can be expressed in terms of the time it takes for a particular amount of BrO3 ' to be used up. In all our reactions, the amount of BrO3 ' that reacts in the time we measure will be constant and small compared to the amounts of any of the reactants, including the BrOs, ion itself. This means that the concentrations of all reactants will be essentially constant in equation 4 , and therefore, so will the rate during each trial. The reaction between BrO3,1,1, and H will be carried out under different concentration conditions. Measured amounts of these ions in aqueous solution will be mixed in the presence of a constant, small amount of S2O32. The time it takes for each mixture to tum blue will be measured. The time it takes to reach the color change will be inversely proportional (that is, the faster the reaction, the shorter the time to turn blue) to the rate of reaction 3 . By changing the concentration of one reactant while keeping the concentrations of the others constant, we can determine how the rate of the reaction varies with the concentration of a particular reactant. This will allow us to determine the order of reaction 3 for reach reactant. Once this is known, we can determine the overall rate constant, k, for the reaction. Experimental Procedure Safety 1. Wear eye protection at all times during this experiment. 2. Be cautious of hot surfaces when preparing water baths. 3. Pay attention to the labels on reagents. Make sure the concentration and identity of the reagent you need matches the one you are using. 4. The waste should be disposed in the Heavy Metal Aqueous Waste bottle in the hood. Dependence of the Reaction Rate on Concentration Part A of this experiment will be performed on the benchtop at room temperature. Use the table below to find the reagent volumes to be used in carrying out the necessary reaction trials to solve for m,n, and p in equation 4 . Start by measuring out about 100mL of each of the listed reagents ( except H2O ) into clean, labeled flasks or beakers. You will use these reagents to prepare your reaction mixtures. Tahlo 1 Ronction Mixtures at Room Temperature Reactions 15 will be performed in the same manner as described in the procedure below. Only the volumes will vary between reactions. 1. With a 10mL graduated cylinder, measure 10mL of 0.010MKI,10mL of 0.0010M Na2S2O3, and 10mL of distilled water into a 125mL Erlenmeyer flask. 2. Rinse your graduated cylinder after measuring all the reagents for the flask prior to measuring a second set of reagents into a large test tybe. 3. Into a large test tube, measure 10mL of 0.040MKBHO3 and 10mL of 0.10MHCl. To this flask, add 3-4 drops of starch indicator solution. 4. Pour the contents of the large test tube into the Erlenmeyer flask and briefly swirl the solutions to mix thoroughly. Begin timing the reaction with a stopwatch immediately upon pouring the contents of test tube into the flask (a cell phone stopwatch will work for this). 5. Continue to gently swirl the solution until the reaction turns blue. Stop the time immediately upon the appeararice of the color change and note the time in seconds. 6. The contents of the flask can be discarded into a waste beaker. The products of this experiment should be placed in the heavy metal aqueous waste jar for disposal. 7. Repeat the above procedure for reaction mixtures 2-5. Do not forget to add the starch indicator to the large test tube before pouring it into the flask each timel Rinse the reaction vessels with distilled water between runs. Repeat any experiments where you did not obtain a reliable time measurement. Processing the Data Write all work/calculations for this section in your lab notebookt This section provides a guide for how to process your data collected in the experiment. You may use the boxes below to help organize yourself but be sure to write all your work for this section in your lab notebook! The following calculation guide should not be submitted as part of your report and any work not in your notebook will be ignored. Equations 3 and 4 from the overview have been repeated here for your convenience: 6I(aq)+BrO3+6H(aq)+3I2(aq)+Br(aq)+3H2O(i) Rate=k[l]m[BrO3]n[H+]p The rate of this reaction can be expressed as the (smali) change in the concentration of BrOs3. [BrO3], that occurs, divided by the time interval t required for the change. The negative sign is to make the rate positive, as [BrO3]is negative, due to the fact that BrO3 is disappearing in the course of the reaction. In all the reaction mixtures, the color change occurred when a predetermined number of moles of BrO3 - has been used up in the reaction. Recall that the "clock" allows you to measure the time required for a fixed number of moles of BrO3 ' to react. This time, t, is the rate of the reaction under a given set of conditions. We are going to determine reaction order and k using relative rates rather than absolute rates. For convenience, we will take all relative rates to be 1000/t. Fill in the table in your report form with the reaction rate data from your lab notebook, calculating the relative reaction rate for each mixture. We now need to find the order of reaction for each reactant and the overall rate constant for the reaction. Since we are working with relative rates, we can modify equation 4 as follows: RelativeRate=k[I]m[BrO3]n[H+]p (Eqn7) The relative rate constant, k, and the reaction orders m,n, and p need to be determined in a way consistent with the data in the table. To do this, note that each mixture in reactions 2-4 differ from the mixture in reaction 1 in the concentration of only one species. This means that for any pair of mixtures that includes reaction 1 , there is only one concentration that changes. From the ratio of relative rates for a given pair of mixtures we can find the order for the reactant whose concentration was changed. Follow the steps provided below. Using Equation 7 for reaction mixtures 1 and 2 , substitute the relative rates and concentrations of each ion based on your data table above. as needed. Part A: Dependence of the Reaction Rate on Concentration -hin helow with your data from each reaction conducted in the procedure. Note that Average K : Using the reactant concentrations from reaction mixture 5 , you m,n, and p values, and your determined average K, calculate the time it should take for the reaction to undergo a color chanas How does it compare to the actual time reported in your table above? Experiment 4A - lodine Clock: A Study of Reaction Rates Overview The rate at which a chemical reaction proceeds depends on several factors: the nature of the reaction, the concentrations of the reactants, the temperature, and the presence of possible catalysts. For a given reaction, the rate typically increases with an increase in the concentration of any reactant. The relation between rate and concentration is a simple one, in most cases. As an example, consider the reaction: aA+bBcC The rate of this reaction can usually be expressed by the equation: Rate=k[A]m[B]n (Eqn 1) where m and n are usually (but not always) integers, specifically with values of 0,1,2, and rarely 3. The concentrations of A and B (in moles per liter, M ) are represented as [A] and [B], and k is a constant, called the rate constant of the reaction, which makes the reaction quantitatively correct. The numbers m and n are called the orders of the reaction with respect to A and B. If m is 1 , the reaction is said to be first order with respect to the reactant A. If n is 2 , the reaction is second order with respect to reactant B. The overall order is the sum of m and n. In this example, the reaction would be third order overall. In this experiment, we will study the kinetics of a reaction that is part of a family of reactions commonly called an "iodine clock." These reactions are so named because when combined with a starch indicator, the colorless iodide ion becomes triiodide in the course of the reaction, and combines with the starch producing a sudden, intense color change to dark blue. This color is visible to the naked eye when the concentration of triiodide ion exceeds 105M. The reaction that we will be studying is as follows: 6I(aq)+BrO3+6H(aq)+3I2(aq)+Br(aq)+3H2O(q)(Eqn2) The rate law of this reaction can therefore be expressed as: Rate=k[I]m[BrO3]n[H+]p where m,n, and p are the orders of the reaction with respect to iodide, bromate, and hydrogen ion, and k is the rate constant of the reaction. To obtain a time delay with a sharp color change, we introduce a "clock" into the reaction in the form of a reducing agent, thiosulfate. This reaction is as follows: I2(aq)+2S2O3(aq)22I(aq)+S4O6(aq)2 Relative to reaction 3 , this reaction is practically instantaneous. The molecular iodine produced in reaction 3 reacts completely with the thiosulfate ion, S2O32, so that until all the thiosulfate ion has reacted completely, the concentration of iodine remains effectively zero. As soon as the thiosulfate ion is consumed, the iodine produced by 3 begins to accumulate in the solution. The presence of iodine becomes immediately apparent because even small concentration of lodine causes the indicator to turn a deep blue color. The "clock" tells us when a given amount of BrO;' ion has reacted ( 1/6 mole of BrOs' per mole of S2O322 ). Importantly, the rate of reaction can be expressed in terms of the time it takes for a particular amount of BrO3 ' to be used up. In all our reactions, the amount of BrO3 ' that reacts in the time we measure will be constant and small compared to the amounts of any of the reactants, including the BrOs, ion itself. This means that the concentrations of all reactants will be essentially constant in equation 4 , and therefore, so will the rate during each trial. The reaction between BrO3,1,1, and H will be carried out under different concentration conditions. Measured amounts of these ions in aqueous solution will be mixed in the presence of a constant, small amount of S2O32. The time it takes for each mixture to tum blue will be measured. The time it takes to reach the color change will be inversely proportional (that is, the faster the reaction, the shorter the time to turn blue) to the rate of reaction 3 . By changing the concentration of one reactant while keeping the concentrations of the others constant, we can determine how the rate of the reaction varies with the concentration of a particular reactant. This will allow us to determine the order of reaction 3 for reach reactant. Once this is known, we can determine the overall rate constant, k, for the reaction. Experimental Procedure Safety 1. Wear eye protection at all times during this experiment. 2. Be cautious of hot surfaces when preparing water baths. 3. Pay attention to the labels on reagents. Make sure the concentration and identity of the reagent you need matches the one you are using. 4. The waste should be disposed in the Heavy Metal Aqueous Waste bottle in the hood. Dependence of the Reaction Rate on Concentration Part A of this experiment will be performed on the benchtop at room temperature. Use the table below to find the reagent volumes to be used in carrying out the necessary reaction trials to solve for m,n, and p in equation 4 . Start by measuring out about 100mL of each of the listed reagents ( except H2O ) into clean, labeled flasks or beakers. You will use these reagents to prepare your reaction mixtures. Tahlo 1 Ronction Mixtures at Room Temperature Reactions 15 will be performed in the same manner as described in the procedure below. Only the volumes will vary between reactions. 1. With a 10mL graduated cylinder, measure 10mL of 0.010MKI,10mL of 0.0010M Na2S2O3, and 10mL of distilled water into a 125mL Erlenmeyer flask. 2. Rinse your graduated cylinder after measuring all the reagents for the flask prior to measuring a second set of reagents into a large test tybe. 3. Into a large test tube, measure 10mL of 0.040MKBHO3 and 10mL of 0.10MHCl. To this flask, add 3-4 drops of starch indicator solution. 4. Pour the contents of the large test tube into the Erlenmeyer flask and briefly swirl the solutions to mix thoroughly. Begin timing the reaction with a stopwatch immediately upon pouring the contents of test tube into the flask (a cell phone stopwatch will work for this). 5. Continue to gently swirl the solution until the reaction turns blue. Stop the time immediately upon the appeararice of the color change and note the time in seconds. 6. The contents of the flask can be discarded into a waste beaker. The products of this experiment should be placed in the heavy metal aqueous waste jar for disposal. 7. Repeat the above procedure for reaction mixtures 2-5. Do not forget to add the starch indicator to the large test tube before pouring it into the flask each timel Rinse the reaction vessels with distilled water between runs. Repeat any experiments where you did not obtain a reliable time measurement. Processing the Data Write all work/calculations for this section in your lab notebookt This section provides a guide for how to process your data collected in the experiment. You may use the boxes below to help organize yourself but be sure to write all your work for this section in your lab notebook! The following calculation guide should not be submitted as part of your report and any work not in your notebook will be ignored. Equations 3 and 4 from the overview have been repeated here for your convenience: 6I(aq)+BrO3+6H(aq)+3I2(aq)+Br(aq)+3H2O(i) Rate=k[l]m[BrO3]n[H+]p The rate of this reaction can be expressed as the (smali) change in the concentration of BrOs3. [BrO3], that occurs, divided by the time interval t required for the change. The negative sign is to make the rate positive, as [BrO3]is negative, due to the fact that BrO3 is disappearing in the course of the reaction. In all the reaction mixtures, the color change occurred when a predetermined number of moles of BrO3 - has been used up in the reaction. Recall that the "clock" allows you to measure the time required for a fixed number of moles of BrO3 ' to react. This time, t, is the rate of the reaction under a given set of conditions. We are going to determine reaction order and k using relative rates rather than absolute rates. For convenience, we will take all relative rates to be 1000/t. Fill in the table in your report form with the reaction rate data from your lab notebook, calculating the relative reaction rate for each mixture. We now need to find the order of reaction for each reactant and the overall rate constant for the reaction. Since we are working with relative rates, we can modify equation 4 as follows: RelativeRate=k[I]m[BrO3]n[H+]p (Eqn7) The relative rate constant, k, and the reaction orders m,n, and p need to be determined in a way consistent with the data in the table. To do this, note that each mixture in reactions 2-4 differ from the mixture in reaction 1 in the concentration of only one species. This means that for any pair of mixtures that includes reaction 1 , there is only one concentration that changes. From the ratio of relative rates for a given pair of mixtures we can find the order for the reactant whose concentration was changed. Follow the steps provided below. Using Equation 7 for reaction mixtures 1 and 2 , substitute the relative rates and concentrations of each ion based on your data table above. as needed. Part A: Dependence of the Reaction Rate on Concentration -hin helow with your data from each reaction conducted in the procedure. Note that Average K : Using the reactant concentrations from reaction mixture 5 , you m,n, and p values, and your determined average K, calculate the time it should take for the reaction to undergo a color chanas How does it compare to the actual time reported in your table above