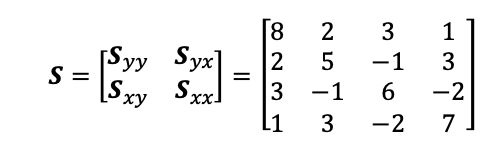Canonical correlation analysis quantifies the correlation between a linear combination of variables in one set with a linear combination of potentially different variables in another set and maximizes such correlation among the space of linear combinations. Use equation (15.6) to give the sample canonical correlations if the sample covariance/variance matrix is:

7 UIN I w Syy Syx 3 S = H W N OO S xy Xx. -1 6 -2 3 -2 715.3 Canonical Correlations In multivariate data, we may have the case that there are two distinct subsets of vectors, with each subset characterizing certain traits of the unit of measurement. As an example, the marks obtained by a student in the examination for different subjects is one subset of measurements, whereas the performance in different sports may form another subset of measurements. Canon- ical correlations help us to understand the relationship between such sets of vector data. Lety' = (yl,y2, - - - ,yp) and x' = (xl,x2,- - - ,xq)be two set ofvectors measured on the same experimental unit. The goal of a canonical correlation study is to obtain vectors a and b such that correlation between y and x is a maximum, that is, Cor(a'y, Hat) is a maximum. The sample covariance matrix for the vector (y, , - - - ,yp,xl, - - - ,xq) is S: (g: :3") , (15.5) where S\" is the sample covariance matrix of Y, Sn, is the sample covariance matrix between X and Y, yand Sn of X. A measure of assocranon between the y's and the x's is given by 33,: |s"s s-'s,,|=1'[r, (15.6) i=1 where s- min(p, q), and 12,13,- -,r2 are the eigenvalues of 8;), IS x138 15,}, .Note that the asso- ciation measure R2 will be a poor measure since each of the .values 1s between 0 and 1, and hence the product of such numbers approach 0 faster. However, the eigenvalues provide a useful measure of association between the vectors. Particularly, the square root of the eigen- values leads to useful interpretations of the measures of the association. The collection of the square root of the eigenvalues {r1, r2, , r3} has been named the canonical correlations in the multivariate literature. Without loss of generality we assume that r? 2 r; 2 .. . 2 I}. As mentioned in Rencher (2002), the best overall measure of association between the x's and y' s is the largest squared canonical correlation r2. However, the other eigenvalues {iv-2, r} leading to the squared canonical correlations {lrz,. .. ,1-2} also provide measures of supplemental dimensions of linear relationships between the x' s and y' s The two important properties of canonical correlations as listed by Reneher are the following: o Canonical correlations are scale invariant, scales of the it's as well as the y's. o The rst canonical correlation rl is the maximum correlation among all linear combinations between the x's and the y's. See Chapter 1 1 of Rencher for a comprehensive coverage of canonical correlations. We can test the independence of the x' s and the y's using any of the four tests discussed in Section 14.6. The concepts are illustrated for the Chemical Dataset of Box and Youle (1955) and are illustrated in Rencher