Answered step by step
Verified Expert Solution
Question
1 Approved Answer
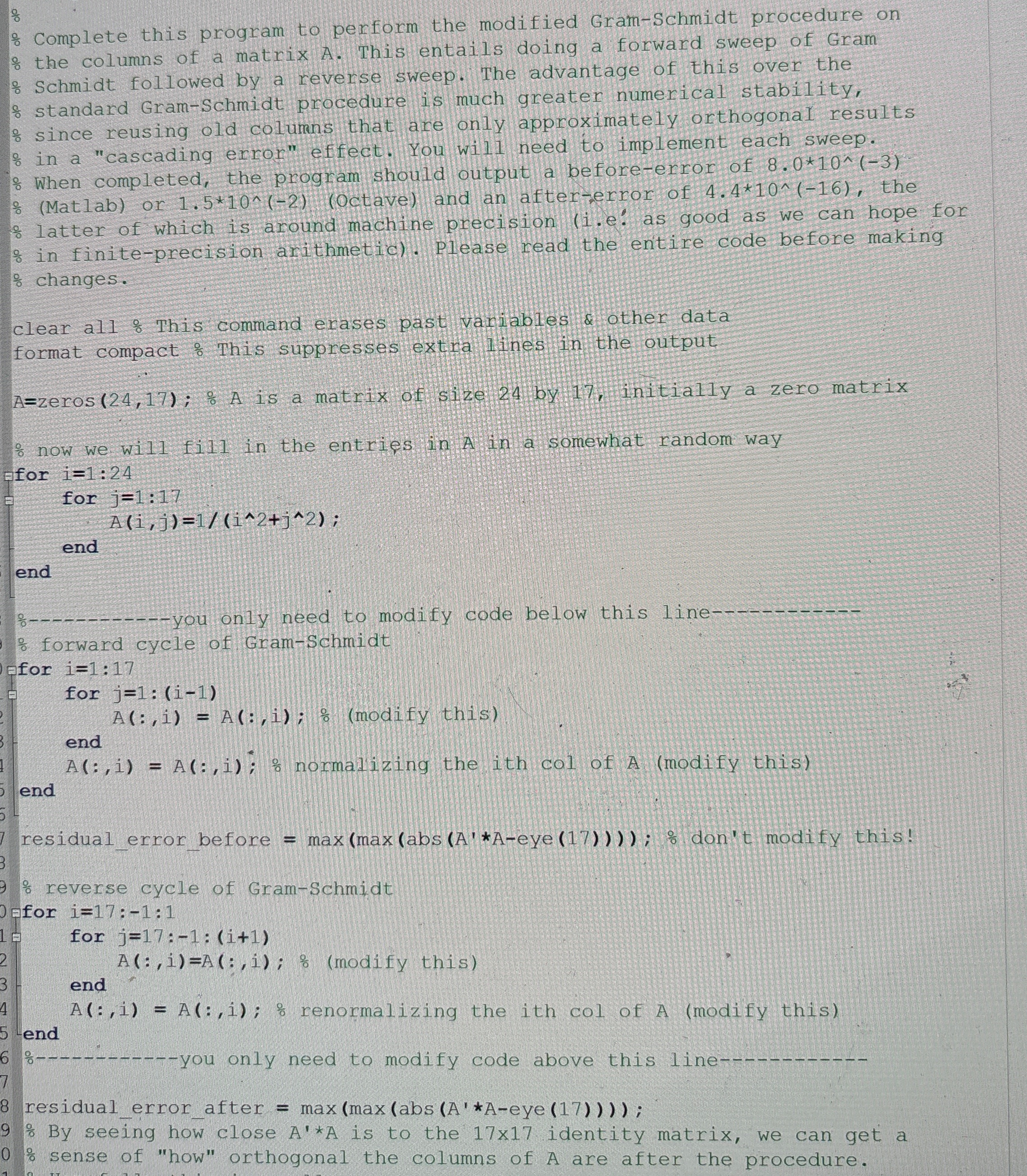
% Complete this program to perform the modified Gram - Schmidt procedure on % the columns of a matrix A . This entails doing a
Complete this program to perform the modified GramSchmidt procedure on the columns of a matrix A This entails doing a forward sweep of Gram
Schmidt followed by a reverse sweep. The advantage of this over the
standard GramSchmidt procedure is much greater numerical stability,
since reusing old columns that are only approximately orthogonal results
in a "cascading error" effect. You wil need to implement each sweep.
When completed, the program should output a beforeerror of
: Matlab or Octave and an aftererror of the
latter of which is around machine precision ie: as good as we can hope for
in finiteprecision arithmetic Please read the entire code before making
changes.
clear all : This command erases past variables & other data
format compact : This suppresses extra Iines in the output
zeros; A is a matrix of size by initially a zero matrix
now we will fill in the entries in A in a somewhat random way
Efor :
for :
end
end
: forward cycle of GramSchmidt
for :
for :
this
end
::; normalizing the ith col of A modify this
end
residualerrorbefore maxeye; don't modify this!
reverse cycle of GramSchmidt
for ::
for ::
:;; modify this
end
::; renormalizing the ith col of modify this
end
residualerrorafter maxeye;
By seeing how close is to the identity matrix, we can get a
sense of "how" orthogonal the columns of A are after the procedure.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


