Question: (computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E has at

(computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E has at least one end in U.

We'll define the following function:f(G,v)=minimal vertex cover that v belongs to

the input is an undirected graph G and a vertex v of G.

The function returns an natural number, that is the smallest size of vertex cover in G that v belongs to

1)Prove: If it is possible to compute f in a polynomial time then P=NP

2)Prove: If it is possible to estimate function f in a constant +5 in polynomial time then P=NP (meaning: if it is possible to calcualte function g(G,v) in a polynomial time, and it is guarenteed that 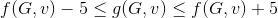(computability and complexity): A vertex cover in an undirected graph G=(V,E) is , then P=NP.

f(G,V) - 5

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

(computability and complexity): A vertex cover in an undirected graph G=(V,E) is a set of vertices U, so that every edge in E Whas at least one end in U. We'll define the following...

We have an undirected graph G =(V. E) with |V players, in which each player i controls exactly one, distinct vertex Vi e V. Each edge e E is associated with a nonnegative weight we. A cut is a...

(9 pts) Problem 20 in Chapter 4 (Greedy Algorithms). The input is a (undirected) graph where the nodes are towns and the edges represent the roads between them. Each edge is labeled with the maximum...

PROBLEM 2: VERTEX COVER Consider the following language from the text, VERTEXCOVER G, k) G is an undirected graph that has a k-node vertex cover] A k-node verter cover of a graph G- (V, E) is a set...

(a) A user complains that their web application Times Out after successfully connecting to a remote host, yet, an investigation with ping indicates the remote host is alive. Propose a cause of this...

There is an underlying undirected graph G = (V, E) with weights on the vertices, where the weight on vertex v is denoted by wv = d(v) (the degree of the vertex). Your goal is to find a vertex cover...

= Question 3: As input, we are given an undirected graph G (V, E) and a set of tokens T, where T| > |El. We have to assign a token t(e) e T to every edge e E E in such a way that: for every token t...

ertex Cover. Given an undirected graph G = ( V , E ) , a Vertex Cover is a set of vertices V V such that every edge e in E is incident on ( touches ) some vertex in V .

A path cover of a directed graph G = (V, E) is a set P of vertex-disjoint paths such that every vertex in V is included in exactly one path in P. Paths may start and end anywhere, and they may be of...

The refractive index of a certain glass is 1.66. For what incident angle is light reflected from the surface of this glass completely polarized if the glass is immersed in (a) Air and (b) Water?

ENU certain company is planning its production and the workforce levels for the months from March until August. Forecasted demand for these periods are, 918, 453, 598, 1,106, 1,989, and 1,130. At the...

How do you do C ) D ) E ) ? Tell me which rule to use for each step ONLY using the allowed rules

Suppose Standard Inc. had the following stock prices from to to ts. Compute (i) the monthly returns over the given sample period, (ii) the expected return, and (iii) standard deviation. Price...

8. Explain the relationship between communication and context.

d. How were you expected to contribute to family life?

2. Analyzing Cultural Patterns. Find a text or speech that discusses some intercultural or cultural issues, and analyze the cultural patterns present in the text. Consider, for example, the I Have a...