Consider a circular road that has n toll booths and n reward booths. At each toll both, you have to pay $1. If you have no money, you are stuck and cant go. However, at each reward booth, you collect $1. You start out with no money, but you decide where to start. You have no choice of direction: you must move clockwise. Prove by mathematical induction that for every n 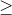0, no matter how the booths are arranged, there is always a starting point that will allow you to go all the way around.

HINTS: (1) To prove the inductive case, remove two carefully chosen booths (2) You have no choice of direction: you must move clockwise. Your only choice is the starting point. (3) Your predicate P(k+1) that you want to prove is that FORALL booth arrangements with k+1 tolls and k+1 rewards, EXISTS a starting point. So you are given such a road and you have to find a starting point. (4) By the inductive hypothesis P(k), you know that FORALL booth arrangement with k tolls and rewards, EXISTS a starting point. So think of an inductive hypothesis like an engineer you can query: if you give her a road with k tolls and k rewards, she'll tell you the starting point. But if you give her k+1 tolls and k+1 rewards, she says nothing. So you have to find a way to cover a toll booth and a reward booth, so that you can use her skills. She'll tell you the starting point for that road with covered up booths. Now you have to use that to find a starting point for the road you are given.