Consider a spherical catalyst particle with radius R. It is surrounded by a uniform film of stationary liquid, which has a thickness . In the liquid solution surrounding the particle and the liquid film, there is a dissolved species A, which has a uniform concentration of C(A0) (Consider the liquid solution to be well-mixed). The liquid solvent is the same in the solution and the film. The system is at a steady state.

Species A is soluble in the liquid film but does not react with any species dissolved in the liquid; it does, however, react at the catalyst particle surface. The reaction follows first-order kinetics, according to which the molar rate of reaction per unit of the catalytic surface area is of the form: R(SA) = -kC(A) , where k is constant. The catalytic surface is impermeable to species A. The catalyst particle and liquid film are spherically symmetrical. (Use the picture below to help see)

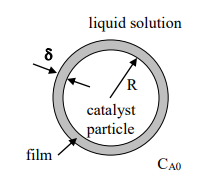
1) Find the conservation equation for species A. Find the boundary conditions that determine the concentration profile of species A in the liquid film.

2) Solve for CA(r) and use the boundary conditions to find any unknown coefficients.

liquid solution 8 R catalyst particle film CA0