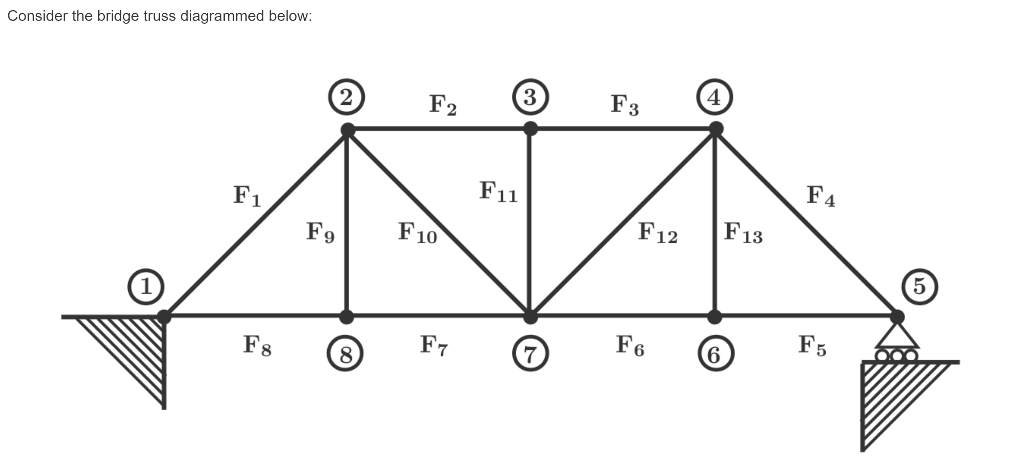
Consider the bridge truss diagrammed below: F11 F 10 F12 F13 F8 Fy @ F6 6 F5 Given a vector of external forces b on the bridge, we can compute the forces Fi, F2, ..., Fia (the forces on each girder) by solving the system Af = b, where f is the vector of unknown forces and A is a 13 x 13 matrix given in the file "bridge_matrix.mat". You can access this matrix by using the command load('bridge_matrix.mat'). After you run this command, you will see a matrix A in your workspace. (Note that this will just work on Matlab grader, but you will have to download the file "bridge_matrix.mat" before you can load it on your own computer.) We will solve for the unknown forces assuming that there are three vehicles at positions 6, 7 and 8 with weights 5 tons, 10 tons and 4 tons, respectively. This means that there is a weight of 5 tons pulling down on girder 13, a weight of 10 tons pulling down on girder 11 and a weight of 4 tons pulling down on girder 9, so we need to use b = [0,0,0,0,0,0,0,0,4,0. 10,0,577. (Remember that the T just means transpose - it means that b is a 13 x 1 column vector with the given entries.) 1. Solve for f using LU-decomposition (i.e., use the lu command). Save the intermediate vector y in a variable named ans1. (See lecture 10.mlx for a reminder about what y is.) 2. Now use the backslash command directly (i.e., without using L, U or P) and save your answer f in a variable named ans2. 3. Now suppose that we add weight to the tuck in position 8 (which corresponds to the 9th entry of b) in increments of 0.01 tons until the bridge collapses. Each girder can withstand 30 tons of compression or tension (i.e., positive or negative forces) before breaking. This means that the bridge will collapse when the absolute value of the largest force in f is larger than 30. Find the smallest weight of the truck at position 8 for which the bridge collapses and save this weight in a variable called ans3. (When the truck has this weight, one of the forces on the bridge should be larger than 30 in absolute value.) Hint: You will probably want to use the functions max and abs. Consider the bridge truss diagrammed below: F11 F 10 F12 F13 F8 Fy @ F6 6 F5 Given a vector of external forces b on the bridge, we can compute the forces Fi, F2, ..., Fia (the forces on each girder) by solving the system Af = b, where f is the vector of unknown forces and A is a 13 x 13 matrix given in the file "bridge_matrix.mat". You can access this matrix by using the command load('bridge_matrix.mat'). After you run this command, you will see a matrix A in your workspace. (Note that this will just work on Matlab grader, but you will have to download the file "bridge_matrix.mat" before you can load it on your own computer.) We will solve for the unknown forces assuming that there are three vehicles at positions 6, 7 and 8 with weights 5 tons, 10 tons and 4 tons, respectively. This means that there is a weight of 5 tons pulling down on girder 13, a weight of 10 tons pulling down on girder 11 and a weight of 4 tons pulling down on girder 9, so we need to use b = [0,0,0,0,0,0,0,0,4,0. 10,0,577. (Remember that the T just means transpose - it means that b is a 13 x 1 column vector with the given entries.) 1. Solve for f using LU-decomposition (i.e., use the lu command). Save the intermediate vector y in a variable named ans1. (See lecture 10.mlx for a reminder about what y is.) 2. Now use the backslash command directly (i.e., without using L, U or P) and save your answer f in a variable named ans2. 3. Now suppose that we add weight to the tuck in position 8 (which corresponds to the 9th entry of b) in increments of 0.01 tons until the bridge collapses. Each girder can withstand 30 tons of compression or tension (i.e., positive or negative forces) before breaking. This means that the bridge will collapse when the absolute value of the largest force in f is larger than 30. Find the smallest weight of the truck at position 8 for which the bridge collapses and save this weight in a variable called ans3. (When the truck has this weight, one of the forces on the bridge should be larger than 30 in absolute value.) Hint: You will probably want to use the functions max and abs