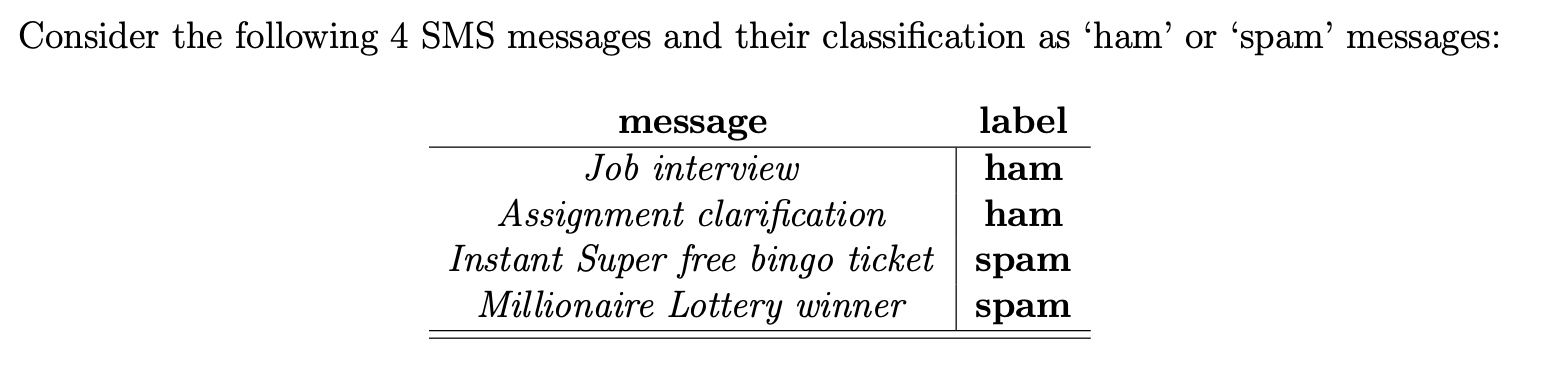


Consider the following 4 SMS messages and their classification as ham' or 'spam messages: message label Job interview ham Assignment clarification ham Instant Super free bingo ticket spam Millionaire Lottery winner spam Using the above messages, construct a Nave Bayes classifier to classify new SMS messages. In particular: 1. Compute the prior probabilities of a new SMS message being 'spam' or 'ham. (These are just the empirical probabilities from the four messages above.) 2. For each de-capitalised keyword that appears in your training set (that is, 'job', inter- view', 'assignment, clarification', 'instant', 'super', 'free', 'bingo', 'ticket', 'millionaire', lottery' and 'winner'), build a frequency table that records the likelihoods P(W|ham), P(-W|ham), P(Wspam) and PG-Wspam). Tip: Remember Laplace's estimator! Just like a likelihood of 0, a likelihood of 1 is troublesome as its negation is 0. This is not a concern for big data sets as no word is likely to appear in every message. To avoid this issue in our toy example, replace any likelihood smaller than 0.05 (larger than 0.95) with 0.05 (0.95). This can be regarded as a variant of the Laplace estimator. Now you can use the Nave Bayes algorithm to make predictions. Predict if the following two SMS messages are ham or spam: message assignment results free pizza label ? ? This actually turns out to be more cumbersome than expected: For the first SMS message, for example, you need to use the law of total probability as well as the conditional independence to compute the quantity P(-job 1 -interview 1 -assignment A clarification 1 -instant \ -super ^-free 1-bingo 1 -ticket -millionaire 1 Flottery 1 winner/). Afterwards you can compute the quantities P(ham|-job A interview 1-assignment A clarification 1 -instant 1-super ^-free 1-bingo 1 ticket -millionaire 1 lottery 1 -winner-) and P(spam|-job 1 -interview 1-assignment A clarification 1 -instant 1-super A-free 1-bingo 1 -ticket 1 millionaire 1 lottery ^-winner ) using Bayes' Theorem and the conditional independence. Alternatively, you can exploit (as explained in the slides) the fact that P(ham|-job 1 -interview 1 ...) P(ham) P(-job|ham) P(-interview ham).. and P(spam|-job 1 -interview 1 ...) P(spam) P(-jobspam) P(-interview spam) ... to calculate propensities that you subsequently scale to probabilities by dividing them with the sum P(ham).P(-job|ham).P(-interview ham).... + P(spam).P(-jobspam).P(-interview/spam).... You can use a spreadsheet to simplify computations if you wish. Make sure that you explain every step, though









