Question: Consider the matrix Find the Eigenvalues of the matrix A. Find two (linearly independent) eigenvectors for this matrix. Show that the two eigenvectors are

Consider the matrix

A= (2 2 -1

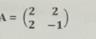
Find the Eigenvalues of the matrix A.

Find two (linearly independent) eigenvectors for this matrix.

Show that the two eigenvectors are perpendicular (by showing that their Inner product. r+ r = 0).

Find a similarity transformation, C, that will diagonally the matrix A (form the matrix C by normalizing the two eigenvectors and then using one of the normalized eigenvectors as the first column and the second normalized eigenvector as the second column).

Show that the matrix C is Unitary.

A= (2 2 -1

Step by Step Solution

★★★★★

3.37 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Finding the eigenvalues of A To find the eigenvalues of A we solve the characteristic equation detA I 0 This gives us the quadratic equation 2 2 1 0 T... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Randy Smith was very proud of his new position as inventory control manager for theJohnson Trinket Company. His primary responsibility had been fairly clearly defined: Maintain an inventory level in...

Consider the following hermitian matrix: (a) Calculate det (T) and Tr (T). (b) Find the eigenvalues of T. Check that their sum and product are consistent with (a), in the sense of Equation A.93....

I am stuck on this problem. I need to know how to solve it and part of that is knowing what I have done wrong in my current attempts to solve it. I have attached my work, which is incomplete, and a...

Each of the following statements is either True or False. Please clearly indicate True or False in the below. All questions have equal weight. Consider a probabilistic model with a sample space 2, a...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

6. Recall that a unitary matrix U satisfies Uf = U=1. (a) Prove that the eigenvalues of a unitary matrix must all have [A|2 = 1, where here J..| is the complex magnitude. Note that this means A = e"...

Please help me with parts (d) and (e), thanks. Eigenvectors and Diagonalization (a) Let A be an n x n matrix with n linearly independent eigenvectors 71, 72, ..., Un, and corre- sponding eigenvalues...

explain how this application would be related to industrial engineering PART 1 (60 points) - Image compression and data analysis Figure 1: Lena. The digital images are represented with matrices. Each...

a) Determine the poles and zeros of the system and show them on the complex plane. (Hint: You may use roots() and pzmap() command of MATLAB.) b) Considering the locations of the poles, comment on the...

Provide an example of a way that King Rex failed at making "good" law, according to Fuller (1964).

When actual revenue compared to budgeted revenue is lower than expected, one would expect the food cost percentage to also be lower. True False

Construct a sequence of real numbers x0, x1 ...... such that any c [0, 1] is the limit of some subsequence of the sequence you constructed. A 25pF parallel-plate capacitor with an air gap between...

How are the tastes, or demand preferences, of a nation introduced in this chapter? Why are they needed?

Design two simple algorithms for bit-stuffing. The first adds bits at the'sender; the second removes bits at the receiver.

A retail company must file a monthly sales tax report listing the total sales for the month, and the amount of state and county sales tax collected. The state sales tax rate is 4% and the county...

A software company sells three packages, Package A, Package B, and Package C, which retail for $99, $199, and $299, respectively

Which of the following best distinguishes the traditional marketing mix from its modern evolution in marketing management?The modern marketing mix concentrates solely on short-term sales promotions...

Let A be a 5 5 nonsymmetric matrix with rank equal to 3, let B = ATA, and let C = eB. (a) What, if anything, can you conclude about the nature of the eigenvalues of B? Explain. What words best...

Given (a) Find an elementary matrix E such that EA = B. (b) Find an elementary matrix F such that AF = C. (2 1 3 2 1 3 3 B = |1 3 2 7 3 5 2. 4 2 7 -5 3 5 %3D

Show that the elimination method of computing the value of the determinant of an n n matrix involves [n(n - 1)(2n - l)]/6 additions and [(n - 1)(n2 + n + 3)]/3 multiplications and divisions.

Why were Captain Jim Miranda and Todd Williamson successful? Was it just their perseverance, or are there other reasons for their success?

A manager has decided to use the Hawthorne Studies to improve productivity in an office. How would she accomplish this? Would the results be short- or long-term? Explain.

Please evaluate this scenario by detailing what the manager would do for each step in the decision-making process. i) Two employees are blaming each other for a project they collaborated on which...