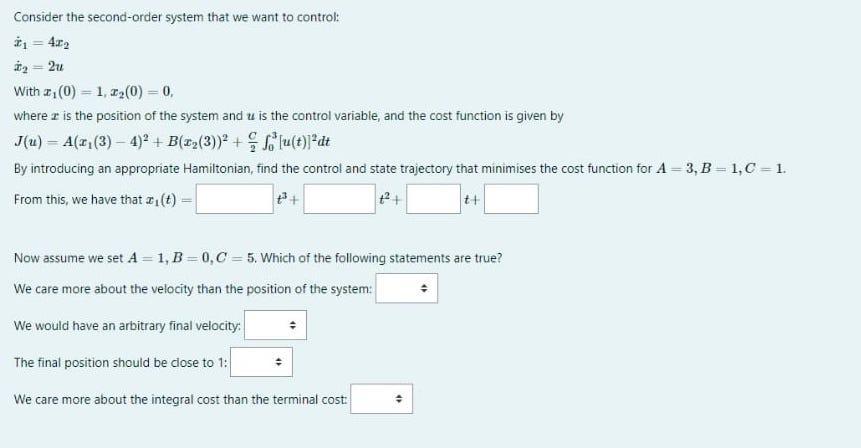
Consider the second-order system that we want to control: i = 4r2 ta = 2u With z (0) = 1, 12(0) = 0, where z is the position of the system and u is the control variable, and the cost function is given by J(u) = A(x (3) - 4) + B(r2(3))* + lu(t)*dt By introducing an appropriate Hamiltonian, find the control and state trajectory that minimises the cost function for A = 3, B = 1,C = 1. From this, we have that e1 (t) = t+ Now assume we set A = 1, B = 0,C = 5. Which of the following statements are true? We care more about the velocity than the position of the system: We would have an arbitrary final velocity: The final position should be dose to 1: We care more about the integral cost than the terminal cost