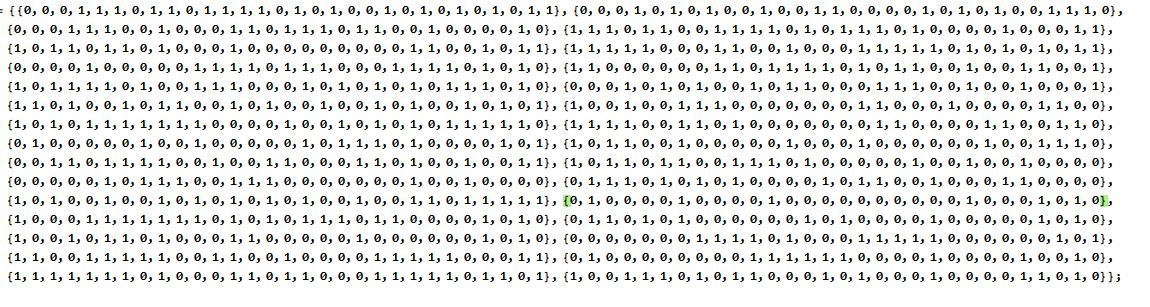Corrosponding adjacency matrix:
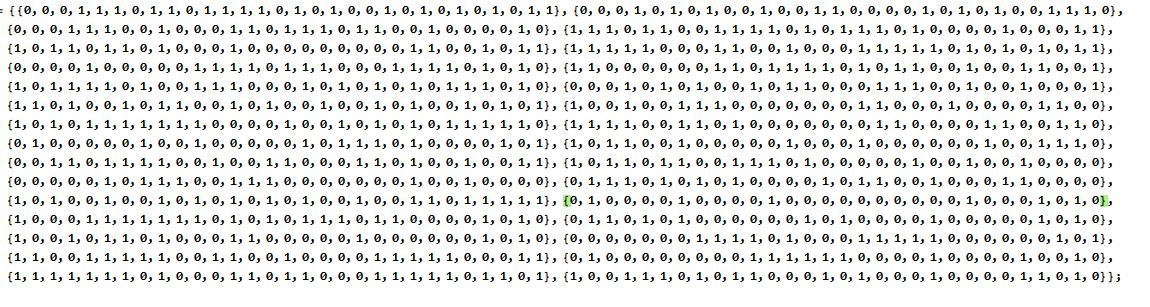
2. We call an undirected graph a basic graph if its adjacency matrix is such that all diagonal entries are zero and all off-diagonal entries are less than or equal to one. Let G=(V, E) be a basic graph. We call any set of three distinct vertices {u, v, w} CV a trinity, if each pair of vertices in the set is connected by an edge. (a) Find an expression for the number of trinitys contained in a basic graph, in terms of the trace of an appropriate matrix. (b) For the graph corresponding to the specific adjacency matrix given on Moodle, use Mathematica and your formula from Part 2a to determine the number of trinitys. {{0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1}, {0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0}, {0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0}, {1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1}, {1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1}, {1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1}, {0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1}, {1, 0, 1, 1, 1, 1, 2, , 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 2, 3, 9}, {0, 0, 0, 1, 2, , 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1} , (1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1), (1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0}, (1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0}, {1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0}, {0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1}, {1, 2, 3, , , , 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 2}, (0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1), (1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0], [0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0], (1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1}, {0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0}, (1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0}, (1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1}, (1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1}, {0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0}, (1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1), (1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0} }; 2. We call an undirected graph a basic graph if its adjacency matrix is such that all diagonal entries are zero and all off-diagonal entries are less than or equal to one. Let G=(V, E) be a basic graph. We call any set of three distinct vertices {u, v, w} CV a trinity, if each pair of vertices in the set is connected by an edge. (a) Find an expression for the number of trinitys contained in a basic graph, in terms of the trace of an appropriate matrix. (b) For the graph corresponding to the specific adjacency matrix given on Moodle, use Mathematica and your formula from Part 2a to determine the number of trinitys. {{0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1}, {0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0}, {0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0}, {1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1}, {1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1}, {1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1}, {0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1}, {1, 0, 1, 1, 1, 1, 2, , 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 2, 3, 9}, {0, 0, 0, 1, 2, , 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1} , (1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1), (1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0}, (1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0}, {1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0}, {0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1}, {1, 2, 3, , , , 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 2}, (0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1), (1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0], [0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0], (1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1}, {0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0}, (1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0}, (1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1}, (1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1}, {0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0}, (1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1), (1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0} }