COST FUNCTION ESTIMATION

Shipping costs are pretty competitive, they are driven heavily by the distance needed to deliver the goods, and the weight of the shipment. Of course, gasoline costs matter, and those are well approximated by the global price of oil. The following cost function is estimated using the following:

TotalCost= 0+1miles+2miles2+3weight+4weight2+5Oil

This relationship can be estimated from their logs of shipping cost data.

Optional: The code PS7_demo.R calls the cost data and estimates, and if you like you can run the code to follow along.[1]

Using regression analysis to estimate the function yields:

[1] In the R program, total cost appears in the dataset as the variable totalinvoiced, the miles the product is shipped is given by miles, miles^2 is milessq; the weight of the goods (in pounds) being shipped is finweight; and the weight^2 is weightsq; and finally the world spot price of West Texas Intermediate oil is given by oil.

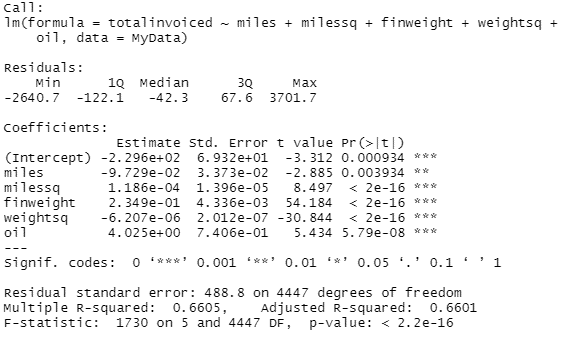
Im going to do a little rounding and put this equation into the below:

TotalCost= -230-0.0973miles+0.000119miles2+0.235weight-0.0000062weight2+4.025Oil

When done correctly, you should find that the estimated total cost when miles=738, weight=2787, and oil=81 is about $695.8175. Answer the following, including your work in the R-code.

a).What is the estimated fixed cost of a shipment? Conceptually, that is the cost if a shipment never traveled any miles, had no weight, and consumed no oil.[1]

b).What is the amount of variable costs when miles=738, weight=2787, and oil=81?

c).What is the average total cost per mile when miles=738, weight=2787, and oil=81?

d).What is the average total cost per pound when miles=738, weight=2787, and oil=81?

[1] This will yield a strange answer and that is a useful thing to reflect on. As you have/will learn in a class that teaches regression analysis, regressions are inferred from observational data. Therefore, it tends to produce good estimates of average observations that occur. In this case, however, the data doesnt show us any trips that never travel any miles, have any weight, or consume any oil. This is a out-of-sample prediction and it is probably not a very good one. It is probably not the case that you can receive a payment to not ship any goods, so if you had to identify fixed costs, relying on the regression model here would probably not be a very smart thing to do.