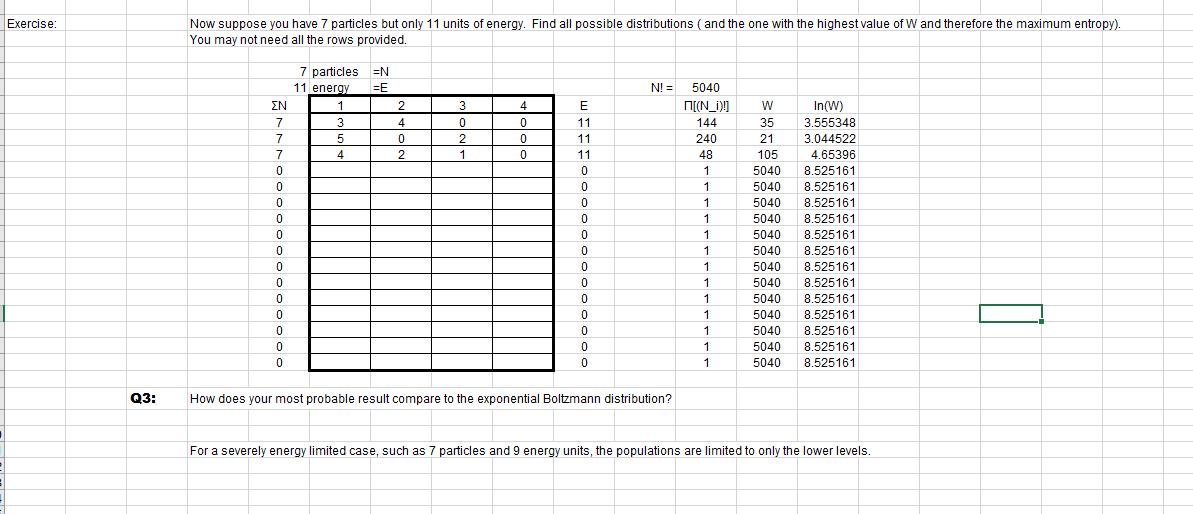
1 Boltzmann's Epitaph, an idea to die for!?! 2 At the beginning of the 20th century, Ludwig Boltzmann was one of the young physicists championing the particle view of matter. 3 Strange as it may seem now, the view was far from universal at that time, indeed it was not the favored theory of matter. The heavyweights of the time, 4 like Ernst Mach and others were strongly opposed to the idea and presented a strong resistance to the ideas at scientific conferences. 5 One unfortunate result of this was Ludwig Boltzmann's suicide at one such conference when he was still in his twenties. 6 His statistical formula for entropy is engraved on his headstone in memmory of his achievement and, perhaps, in mourning of 7 what might have been accomplished had he continued his work. 8 7 9 10 Without presenting a formal derivation, Boltzmann's formula for entropy is 11 S = klnW W = 12 13 Basically, it says that the arrangement with the greatest entropy is the one which is most probable. 14 Recall that the change in entropy for an isolated system is always greater than zero. 15 So, isolated systems tend toward the most probable distribution of energy. 16 number of arrangements of the energy with = N! / [N1! N2! N3!...] W is called the partition function. 17 One application of this is for molecules with discrete energy states as required by quantum mechanics. 18 The fraction of molecules or population in each energy state can be determined using Boltzmann's entropy. 19 40 20 Start with N molecules at temperature T 21 and in some energy state En 31 32 33 34 [Q2] E_therm =1.5 NKT E_tot = N(1.5kT+En) 22 22 23 Via collisions and so on, the energy will not remain distributed this way. 24 35 36 37 38 k=R/N_A 25 We will suppose that the processes which redistribute the energy happen with no change in total energy. 26 This is just saying that there is no energy input or output from the collection of molecules, 27 so that it is an isolated system.. 28 29 30 [Q1] For a total of N particles, there are N! ways of arranging them: N choices for the first (N-1) for the second....1 for the last If the N objects are placed in distinct groups, then each of these groups will have a number of arrangements calculated the same way. N1 objects in the first group can be arranged N1! Ways. These rearrangements do not affect the distribution of objects among the groups, so we divide the total N! arrangements by each of the Ni! Factors to get the number of arrangements with the same distribution. That is the W in Boltzmann's equation. So, picture an isolated collection of N molecules at temperature T and in the energy state En. No energy is exchanged with the surroundings. As some of them get bumped up into other energy states Ei, what happens to the thermal energy of the molecule? We will use the thermodynamic definition of entropy: AS=dQ/T for reversible dQ (as it is here). We will count any change in thermal energy as heat. When a molecule changes energy state from En to Ei, the energy tied up in that form changes by Ei-En. Keeping in mind the statement on line 32, show that the heat associated with the transition is given by Q = -AE. Using that result, show how the following relations come from Boltzmann's entropy equation (the first relation): S=kIn(W) e^S/k = W S=Q/T e^-AE/kt = W This exponential is the ratio of populations for two energy levels AE apart when at thermal equilibrium. Exercise: Q3: Now suppose you have 7 particles but only 11 units of energy. Find all possible distributions (and the one with the highest value of W and therefore the maximum entropy). You may not need all the rows provided. EN 7 7 7 0 0 7 0 0 0 0 0 0 0 7 0 0 0 7 0 0 0 0 0 0 0 0 7 particles 11 energy 1 3 5 4 N =E 2 4 0 2 3 0 2 1 4 0 0 0 E 11 11 11 0 5 0 2 0 5 0 5 0 5 0 5 0 0 0 0 0 0 0 0 0 NI = How does your most probable result compare to the exponential Boltzmann distribution? 5040 [(N_)!] 144 240 48 1 + 1 + 1 + 1 i 1 - 1 - 1 1 1 1 1 1 1 W 35 21 21 105 105 5040 5040 5040 5040 5040 5040 5040 FATA 5040 FATA 5040 FATA 5040 MOTO 5040 5040 5040 5040 5040 5040 5040 5040 In(W) 3.555348 3.044522 4.65396 8.525161 8.525161 505464 8.525161 0 505424 8.525161 0 505424 8.525161 0 505464 8.525161 0 505464 8.525161 0.505464 8.525161 0.505464 8.525161 8.525161 505161 8.525161 8.525161 8.525161 For a severely energy limited case, such as 7 particles and 9 energy units, the populations are limited to only the lower levels.