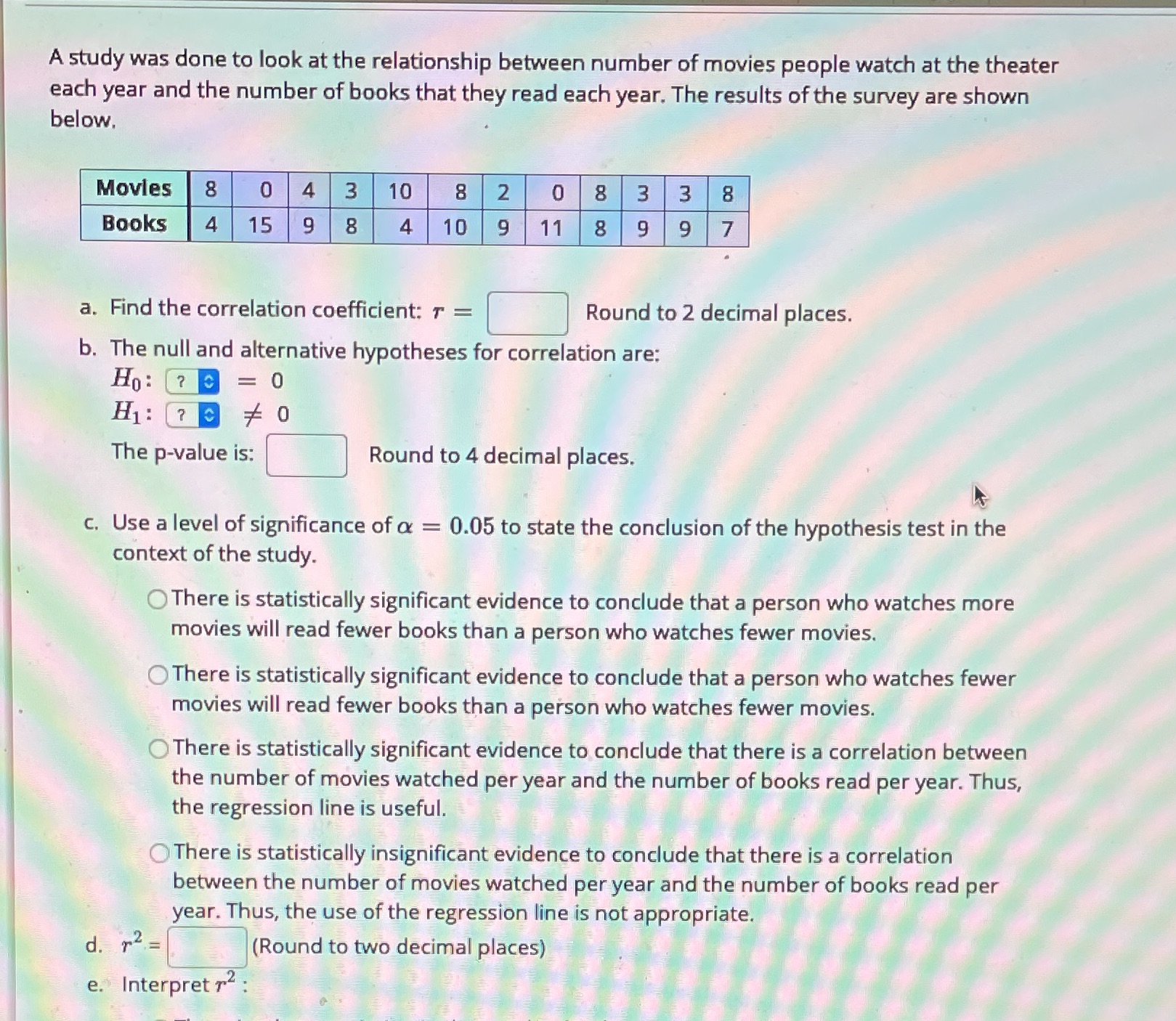
Question
couldn't fit it all in the photo but here's the rest!: f. The equation of the linear regression line is: y^= ?+?x (please show your
couldn't fit it all in the photo but here's the rest!: f. The equation of the linear regression line is: y^= ?+?x (please show your answer to two decimal places)g. use the model to predict the number of books read per year for someone who watches 7 movies per year.books per year= (please round your answer to the nearest whole number)h. interpret the slope of the regression line in the context of the question: 1. The x goes up, y goes down.2. The slope has no practical meaning since people cannot read a negative number of books.3. for every additional movie that people watch each year, there tends to be an average decrease of 0.64 books read. i. if the y-intercept makes sense in this question, then interpret the y-intercept in the context of the question: 1. The average number of books read per year is predicted to be 12 books. 2. The best prediction for a person who doesn't watch any movies is that they will read 12 books each year.3. the y-intercept has no practical meaning for this study. 4. if someone watches 0 movies per year, then that person will read 12 books this year.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


