decision making
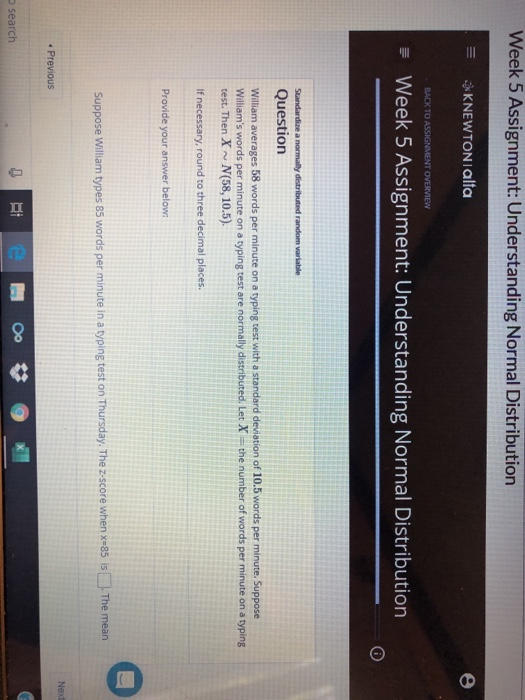
Week 5 Assignment: Understanding Normal Distribution KNEWTONIalta BACK TO ASSIGNMENT OVERVIEW Week 5 Assignment: Understanding Normal Distribution O Standardize a normally distributed random variable Question William averages 58 words per minute on a typing test with a standard deviation of 10.5 words per minute. Suppose William's words per minute on a typing test are normally distributed. Let X - the number of words per minute on a typing test. Then X ~ N(58, 10.5). If necessary, round to three decimal places. Provide your answer below: Suppose William types 85 words per minute in a typing test on Thursday. The z-score when x=85 is . The mean Next . Previous search IIFor problems 5 and 6, The body temperatures of adults have a mean of 98.6 " F and a standard deviation of 0.60 * F. A random sample of 38 adults selected. 5. What is the approximate distribution of I = (the sample average of the 36 temperatures)? (Use Central Limit Theprem.) a) Normally distributed with u=98.6 and a = 0.50. C bl Normally distributed with =16.43 and o = 0.01 c Normally distributed with p=99.5 and o = 0.10 Normally distributed with p=98.6 and o = 0 01 6. Find the probability that their mean body temperature is greater than 98.4 . F. P ( x 7 980 ) a) -2.00 b) 2.00 98 2 _48. 97 90.0228 0.6772Choper & Continuous Probability Distributors The moment-generating function of 2 has the form of a mongil-jobunting func- Linn For a reormal random variable with mean 0 and variance L The. by pup- erty , variable Z must have a normal distribution with mean 0 and varianor I. Exercises 4.140 Show fut a garra duribution with parameters 8.102 Lat I dinghy a standard normal random var 8. 103 Lut & dench a Standard normal random want 4.101 4wing the moment generating function to f What sous thy uniquenous property of the moment-pingsting function full you about the Al times, theoretical distribution of the functions of random variables might not be known to the experimenters, In such situations, the probability distributions cim be simulated for decision making. Most of the modern statistical software arc capable of generating measurements from commonly used distributions. Example 6.33 One particular assembly in bicycles requires inserting a solid bar imo a bellow cylinder. The bicycle manufacturer receives bar and cylinders from two different contractors, The information provided by the contractors says that The bar diameters are approximately normally distributed with moan 2 om and Mandard deviation 0.I cm. " The cylinder's inner diameters any approximately normally distributed with main 2 1 cm and standard deviation 9.03 om. If the bar diameter is larger than the cylinder diameter, the moombly is not possi ble. Also bars with diameter more than 03 cm smaller than the cylinder are too loves to be used in the assembly. If one bar and our cylinder are schooled at ran dom, what is the probability that the assembly is not possibly? Solution Let C= the diameter of the cylinder and & = they diameter of the hur Them - & is approximately normally distributed with a, = 1 omando, =0.I am. . Ch apprecimately normally distributed with ar = 1 1 cm and or = DOsom We are interested in the difference (C - D). The assembly is mex possibly if [C - B)