e7 thx for help

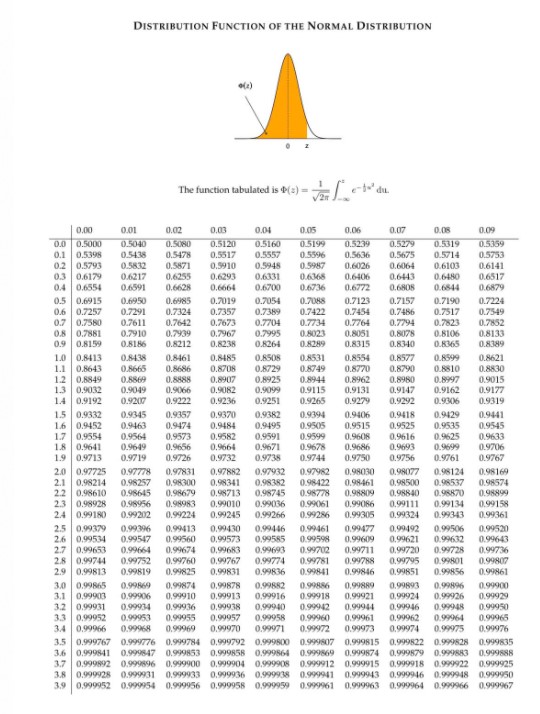
DISTRIBUTION FUNCTION OF THE NORMAL DISTRIBUTION The function tabulated is +() = e- du 0.02 0.03 0.01 0.07 0.09 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 05199 0.5239 0.5279 0.5019 0.5359 0.1 0.5398 0.5438 0.5478 0.5617 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.2 0.5793 0.58.12 0.5571 0.5910 0.5945 0.5947 0.6026 0.6064 0.6103 0.6141 03 0.6179 0.6217 0.6255 0.6293 0.6331 0.6365 0.6-406 0,6443 0.6480 0.6517 04 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.680S 0.6844 0.6879 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7048 0.7123 0.7157 0.7190 0.7224 0.6 0.7257 0.7291 0.7324 0.7357 0.7369 0.7422 0.7454 0.7486 0.7517 0.75-49 0.7 0.7580 0.7611 0.76-42 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8 0.7861 0.7910 0.7939 0,7967 0.7995 0.5023 0.8051 0,8078 0.8106 0.8133 0.9 D.8159 0.8186 0.8212 0.8238 0.6264 0.8289 0.8315 0.8340 0.8365 0.8389 1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 1.1. 0.8643 0.8665 0.8686 0.8708 0.6729 0.8749 0.8770 0.8790 0.8810 0.8830 1.2 0.6849 0.6869 0.8858 0.8907 0.8925 0.8944 0.8962 0.8960 0.8997 0.9015 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.94-41 16 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 17 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 1.H 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9649 0.9706 0.9713 0.9719 0.9726 0.9732 0.9735 0.9744 0.9750 0.9756 0.9761 0.9767 2.0 0.97725 0.97778 0.97831 0.97882 0.97932 0.97962 0.98030 0.98077 0.98124 0.98169 2.1 0.98214 0.98257 0.98300 0.98341 0.98382 0.98422 0.98-461 0,98500 0.98537 0.98574 2.2 0.98610 0.98645 0.98679 0.98713 0.98745 0.96778 0.98809 0.98840 0.93870 0.98899 2.3 0.98928 0.98956 0.98983 0.99010 0.99036 0.99061 0.99086 0,99111 0.99134 0.99158 2.4 0.99180 0.99202 0.99224 0.99245 0.99266 0.99286 0.99305 0.99324 0.993-43 0.99361 2.5 0.99379 0.99396 0.90413 0.99430 0.994 46 0.99461 0.99477 0,99492 0.99506 0.99520 2.6 0.99534 0.99547 0.99560 0,99573 0.99585 0.99598 0.99609 0,99621 0.99632 0.99643 17 0.99654 0.99664 0.99674 0,99683 0.99693 0.99702 0.99711 0,99720 0.99728 0.99736 2.8 0.99744 0.99752 0.99760 0.99767 0.99774 199761 0.99788 0.99795 0.99801 0.99807 20 0.99813 0.99819 0.9982 0.99831 0.99836 0.99841 0.99846 0.99851 0.99856 0.99861 3.01 0.99865 0.99869 0.99874 0,99878 0.99682 0.99856 0,99:889 0,99693 0.99896 0.99900 3.1 0.99903 0.90906 0.94910 0,99913 0.99916 0.99918 0.99921 0,99924 0.99926 0.99929 3.1 0.99931 0.99934 0.99936 0.99938 0,999 40 0.999.12 0.99944 0,999 46 0.999-48 0.99950 3.1 0.99952 0.90953 0.99957 0.99958 0.99960 0.99961 0.99962 0.99964 0.99915 3.4 0.99066 0.99969 0.99970 0.99971 0.99972 0.99973 0,99974 0.99975 0.99976 3.5 0.999767 0.999776 0.999784 0.999792 0.999500 0.999817 0.999815 0,999822 0.999828 0.999835 0.999841 0.999847 0.999853 0.999858 0.999564 0.999569 0.999874 0,999879 0.999683 0.999838 1.7 0.999692 0.999896 0.999900 0.999904 0.999908 0.999912 0.999915 0,999918 0.999922 0.999925 0.999925 0.999931 0.999933 0.999936 0.999938 0.999941 0.999943 0,999946 0.999948 0.999950 0,999953 0.999954 0.939956 0.999958 0.999959 0.999961 0.999963 0,999964 0.999966 0.999967(i) Let X be a random variable whose probability density function is given by 62:\" + e'm, if :r: > 0 :1; : fX( ) {0, otherwise Write down the moment generating function of X. Use this moment generating function to compute the first and second moment. (ii) Let Y be a random variable whose moment generating function is given by Mrs) = (0.3 + 0.7a)\" ,what is Pa 5 Y s 3)? (iii) Suppose that X from (i) is independent of Y from (ii), find E(X 21")