Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Mary's credit card situation is out of control because she cannot afford to make her monthly payments. She has three credit cards with the


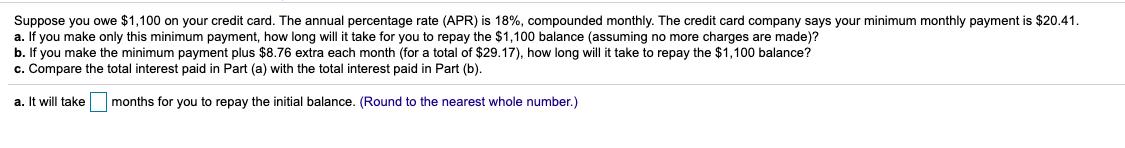


Mary's credit card situation is out of control because she cannot afford to make her monthly payments. She has three credit cards with the following loan balances and APRS: Card 1, $5,000, 20%; Card 2, $5,700, 24%; and Card 3, $3,400, 18%. Interest compounds monthly on all loan balances. A credit card loan consolidation company has captured Mary's attention by stating they can save Mary 17% per month on her credit card payments. This company charges 17.5% APR. Is the company's claim correct? Assume a 10-year repayment period. Mary's current minimum monthly payments are $ (Round to the nearest cent.) You deposit $3,500 at the end of the year (k = 0) into an account that pays interest at a rate of 7% compounded annually. A year after your deposit, the savings account interest rate changes to 12% nominal interest compounded monthly. Five years after your deposit, the savings account again changes its interest rate; this time the interest rate becomes 8% nominal interest compounded quarterly. Eight years after your deposit, the saving account changes its rate once more to 5% compounded annually. a. How much money should be in the savings account 17 years after the initial deposit, assuming no further changes in the account's interest rate? b. What interest rate, compounded annually, is equivalent to the interest pattern of the saving account Part (a) over the entire 17 year period? a. $ should be in the savings account 17 years after the initial deposit. (Round to the nearest dollar.) Suppose you owe $1,100 on your credit card. The annual percentage rate (APR) is 18%, compounded monthly. The credit card company says your minimum monthly payment is $20.41. a. If you make only this minimum payment, how long will it take for you to repay the $1,100 balance (assuming no more charges are made)? b. If you make the minimum payment plus $8.76 extra each month (for a total of $29.17), how long will it take to repay the $1,100 balance? c. Compare the total interest paid in Part (a) with the total interest paid in Part (b). a. It will take months for you to repay the initial balance. (Round to the nearest whole number.) The PHC is offering a prize of $5,000 per week for 3 years. If the interest rate is 10.4%, compounded weekly, what is the present equivalent value of the prize? What is the future equivalent value at the end of 3 years? Assume 52 weeks in a year. The present equivalent value of the prize is $ . (Round to the nearest dollar.) Sarah is going to borrow money for her college expenses. Her local credit union will lend Sarah $10,000 now at a nominal interest rate of 4% per year, compounded quarterly. Then after two years, the credit union will lend her an additional $10,000 at a higher interest rate of 6% per year compounded annually. Sarah will repay these loans over four years when she graduates. How much does Sarah owe the credit union when she graduates 4 years after starting college? Click the icon to view the interest and annuity table for discrete compounding when i= 6% per year. Sarah will owe $ at the end of year 4. (Round to the nearest dollar.) Mary's credit card situation is out of control because she cannot afford to make her monthly payments. She has three credit cards with the following loan balances and APRS: Card 1, $5,000, 20%; Card 2, $5,700, 24%; and Card 3, $3,400, 18%. Interest compounds monthly on all loan balances. A credit card loan consolidation company has captured Mary's attention by stating they can save Mary 17% per month on her credit card payments. This company charges 17.5% APR. Is the company's claim correct? Assume a 10-year repayment period. Mary's current minimum monthly payments are $ (Round to the nearest cent.) You deposit $3,500 at the end of the year (k = 0) into an account that pays interest at a rate of 7% compounded annually. A year after your deposit, the savings account interest rate changes to 12% nominal interest compounded monthly. Five years after your deposit, the savings account again changes its interest rate; this time the interest rate becomes 8% nominal interest compounded quarterly. Eight years after your deposit, the saving account changes its rate once more to 5% compounded annually. a. How much money should be in the savings account 17 years after the initial deposit, assuming no further changes in the account's interest rate? b. What interest rate, compounded annually, is equivalent to the interest pattern of the saving account Part (a) over the entire 17 year period? a. $ should be in the savings account 17 years after the initial deposit. (Round to the nearest dollar.) Suppose you owe $1,100 on your credit card. The annual percentage rate (APR) is 18%, compounded monthly. The credit card company says your minimum monthly payment is $20.41. a. If you make only this minimum payment, how long will it take for you to repay the $1,100 balance (assuming no more charges are made)? b. If you make the minimum payment plus $8.76 extra each month (for a total of $29.17), how long will it take to repay the $1,100 balance? c. Compare the total interest paid in Part (a) with the total interest paid in Part (b). a. It will take months for you to repay the initial balance. (Round to the nearest whole number.) The PHC is offering a prize of $5,000 per week for 3 years. If the interest rate is 10.4%, compounded weekly, what is the present equivalent value of the prize? What is the future equivalent value at the end of 3 years? Assume 52 weeks in a year. The present equivalent value of the prize is $ . (Round to the nearest dollar.) Sarah is going to borrow money for her college expenses. Her local credit union will lend Sarah $10,000 now at a nominal interest rate of 4% per year, compounded quarterly. Then after two years, the credit union will lend her an additional $10,000 at a higher interest rate of 6% per year compounded annually. Sarah will repay these loans over four years when she graduates. How much does Sarah owe the credit union when she graduates 4 years after starting college? Click the icon to view the interest and annuity table for discrete compounding when i= 6% per year. Sarah will owe $ at the end of year 4. (Round to the nearest dollar.) Mary's credit card situation is out of control because she cannot afford to make her monthly payments. She has three credit cards with the following loan balances and APRS: Card 1, $5,000, 20%; Card 2, $5,700, 24%; and Card 3, $3,400, 18%. Interest compounds monthly on all loan balances. A credit card loan consolidation company has captured Mary's attention by stating they can save Mary 17% per month on her credit card payments. This company charges 17.5% APR. Is the company's claim correct? Assume a 10-year repayment period. Mary's current minimum monthly payments are $ (Round to the nearest cent.) You deposit $3,500 at the end of the year (k = 0) into an account that pays interest at a rate of 7% compounded annually. A year after your deposit, the savings account interest rate changes to 12% nominal interest compounded monthly. Five years after your deposit, the savings account again changes its interest rate; this time the interest rate becomes 8% nominal interest compounded quarterly. Eight years after your deposit, the saving account changes its rate once more to 5% compounded annually. a. How much money should be in the savings account 17 years after the initial deposit, assuming no further changes in the account's interest rate? b. What interest rate, compounded annually, is equivalent to the interest pattern of the saving account Part (a) over the entire 17 year period? a. $ should be in the savings account 17 years after the initial deposit. (Round to the nearest dollar.) Suppose you owe $1,100 on your credit card. The annual percentage rate (APR) is 18%, compounded monthly. The credit card company says your minimum monthly payment is $20.41. a. If you make only this minimum payment, how long will it take for you to repay the $1,100 balance (assuming no more charges are made)? b. If you make the minimum payment plus $8.76 extra each month (for a total of $29.17), how long will it take to repay the $1,100 balance? c. Compare the total interest paid in Part (a) with the total interest paid in Part (b). a. It will take months for you to repay the initial balance. (Round to the nearest whole number.) The PHC is offering a prize of $5,000 per week for 3 years. If the interest rate is 10.4%, compounded weekly, what is the present equivalent value of the prize? What is the future equivalent value at the end of 3 years? Assume 52 weeks in a year. The present equivalent value of the prize is $ . (Round to the nearest dollar.) Sarah is going to borrow money for her college expenses. Her local credit union will lend Sarah $10,000 now at a nominal interest rate of 4% per year, compounded quarterly. Then after two years, the credit union will lend her an additional $10,000 at a higher interest rate of 6% per year compounded annually. Sarah will repay these loans over four years when she graduates. How much does Sarah owe the credit union when she graduates 4 years after starting college? Click the icon to view the interest and annuity table for discrete compounding when i= 6% per year. Sarah will owe $ at the end of year 4. (Round to the nearest dollar.) Mary's credit card situation is out of control because she cannot afford to make her monthly payments. She has three credit cards with the following loan balances and APRS: Card 1, $5,000, 20%; Card 2, $5,700, 24%; and Card 3, $3,400, 18%. Interest compounds monthly on all loan balances. A credit card loan consolidation company has captured Mary's attention by stating they can save Mary 17% per month on her credit card payments. This company charges 17.5% APR. Is the company's claim correct? Assume a 10-year repayment period. Mary's current minimum monthly payments are $ (Round to the nearest cent.) You deposit $3,500 at the end of the year (k = 0) into an account that pays interest at a rate of 7% compounded annually. A year after your deposit, the savings account interest rate changes to 12% nominal interest compounded monthly. Five years after your deposit, the savings account again changes its interest rate; this time the interest rate becomes 8% nominal interest compounded quarterly. Eight years after your deposit, the saving account changes its rate once more to 5% compounded annually. a. How much money should be in the savings account 17 years after the initial deposit, assuming no further changes in the account's interest rate? b. What interest rate, compounded annually, is equivalent to the interest pattern of the saving account Part (a) over the entire 17 year period? a. $ should be in the savings account 17 years after the initial deposit. (Round to the nearest dollar.) Suppose you owe $1,100 on your credit card. The annual percentage rate (APR) is 18%, compounded monthly. The credit card company says your minimum monthly payment is $20.41. a. If you make only this minimum payment, how long will it take for you to repay the $1,100 balance (assuming no more charges are made)? b. If you make the minimum payment plus $8.76 extra each month (for a total of $29.17), how long will it take to repay the $1,100 balance? c. Compare the total interest paid in Part (a) with the total interest paid in Part (b). a. It will take months for you to repay the initial balance. (Round to the nearest whole number.) The PHC is offering a prize of $5,000 per week for 3 years. If the interest rate is 10.4%, compounded weekly, what is the present equivalent value of the prize? What is the future equivalent value at the end of 3 years? Assume 52 weeks in a year. The present equivalent value of the prize is $ . (Round to the nearest dollar.) Sarah is going to borrow money for her college expenses. Her local credit union will lend Sarah $10,000 now at a nominal interest rate of 4% per year, compounded quarterly. Then after two years, the credit union will lend her an additional $10,000 at a higher interest rate of 6% per year compounded annually. Sarah will repay these loans over four years when she graduates. How much does Sarah owe the credit union when she graduates 4 years after starting college? Click the icon to view the interest and annuity table for discrete compounding when i= 6% per year. Sarah will owe $ at the end of year 4. (Round to the nearest dollar.)
Step by Step Solution
There are 3 Steps involved in it
Step: 1
Ans 1 Marys current minimum monthly payments is For Card 1 interest loan amount 1interestnumber of p...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


