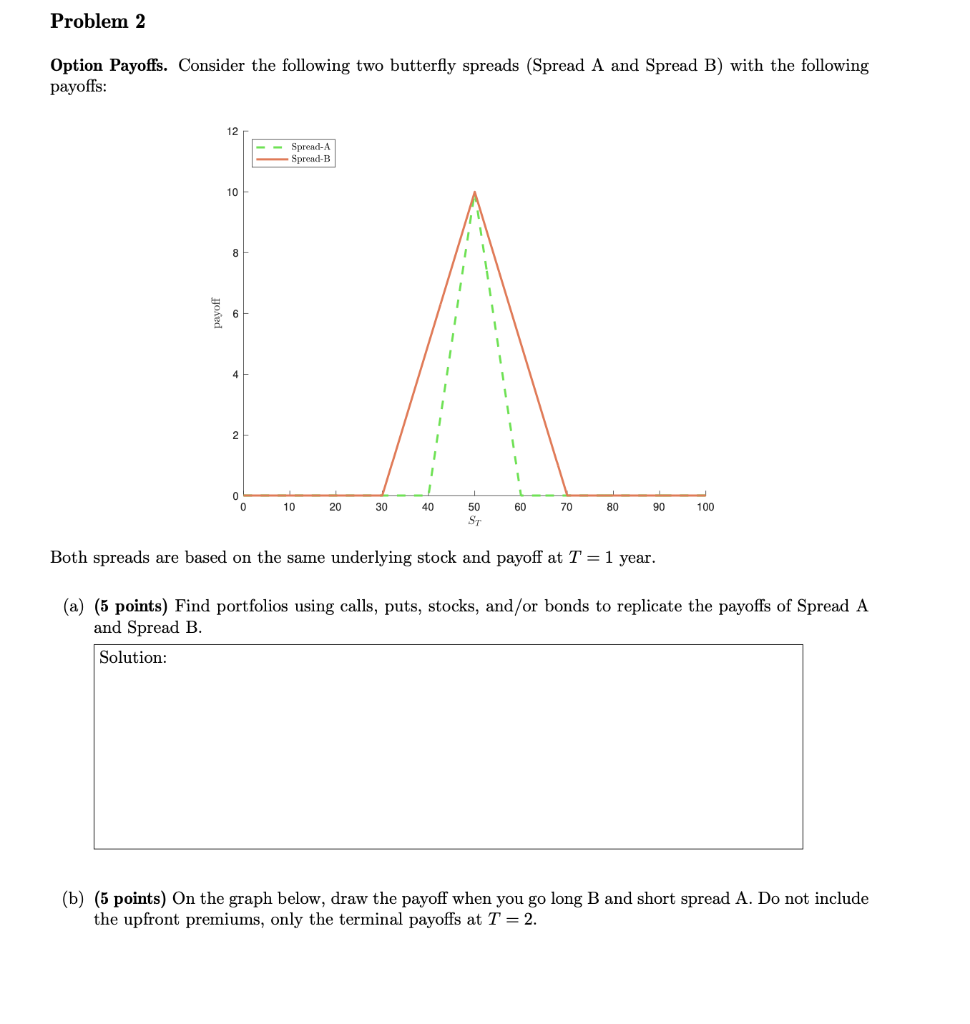
Edit: no further strike details are provided.

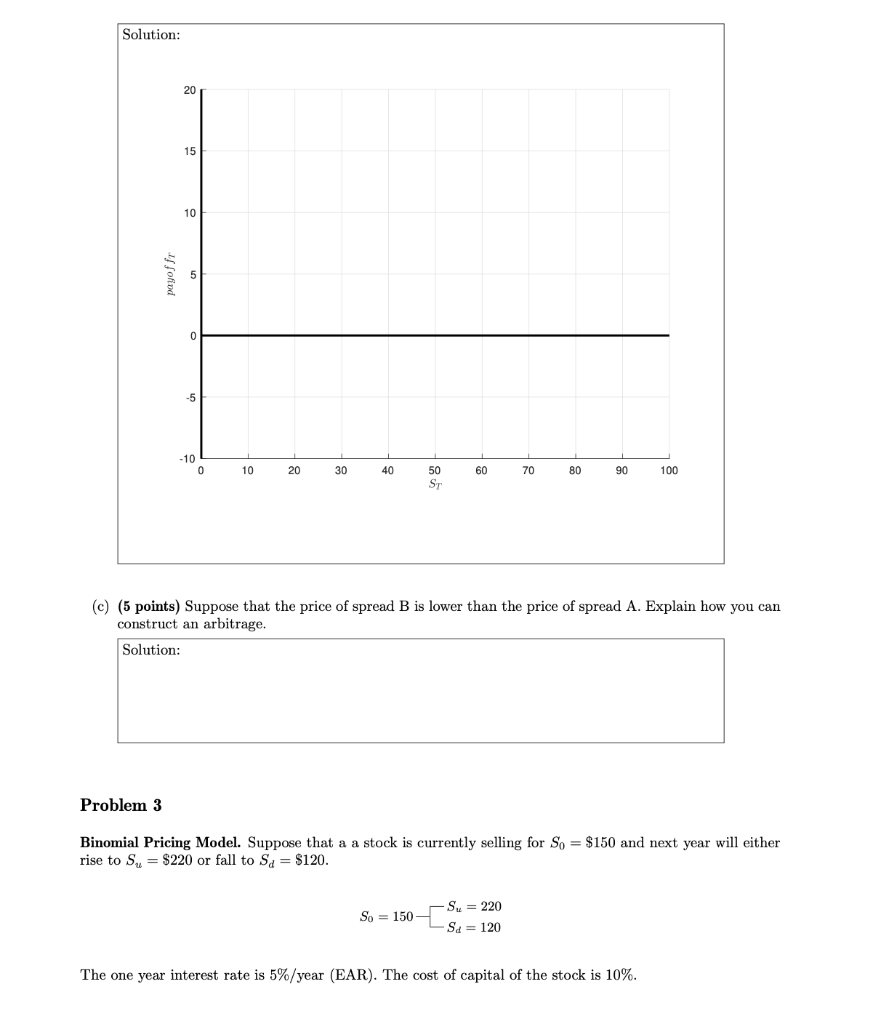
Problem 1 Forwards. Suppose that silver currently trades for $15 per ounce and that you can store silver for two years at a price of $0.10/year, payable at t = 1 and t = 2. Silver provides no convenience yield. The term structure is flat at 5%/year (EAR). (a) (5 points) Find F0,2, the forward price at t=0 to buy the silver at T = 2 years? Solution: (b) (5 points) If silver had a convenience yield (everything else the same), would the forward price you compute above be higher or lower? No explanation is necessary. Solution: (c) (5 points) Suppose that at t = 0, you go short a forward contract to buy 100 ounces of silver. At t=1, the price of silver falls to $10/ounce (storage costs and interest rates stay the same.) Your counterparty declares bankruptcy and the contract is cancelled. Is this good or bad for you? What is the magnitude of the gain or loss to you due to the contract being cancelled? Solution: Problem 2 Option Payoffs. Consider the following two butterfly spreads (Spread A and Spread B) with the following payoffs: 12 Spread-A Spread-B 10 8 1 6 1 1 1 1 1 1 1 1 4 2 1 0 0 10 20 30 40 60 70 80 90 100 50 ST Both spreads are based on the same underlying stock and payoff at T = 1 year. (a) (5 points) Find portfolios using calls, puts, stocks, and/or bonds to replicate the payoffs of Spread A and Spread B. Solution: (b) (5 points) On the graph below, draw the payoff when you go long B and short spread A. Do not include the upfront premiums, only the terminal payoffs at T = 2. Solution: 20 15 10 payoffr -10 0 10 20 30 40 60 70 80 90 100 50 ST (c) (5 points) Suppose that the price of spread B is lower than the price of spread A. Explain how you can construct an arbitrage. Solution: Problem 3 Binomial Pricing Model. Suppose that a a stock is currently selling for So = $150 and next year will either rise to Su = $220 or fall to Sa = $120. So = 150 - Su = 220 Sd = 120 The one year interest rate is 5%/year (EAR). The cost of capital of the stock is 10%. (a) (5 points) Compute the risk-neutral probability of an up movement to have S1 = $220. Solution: (b) (5 points) Compute the price of a call option struck at K=$200. Solution: (c) (5 points) Find a portfolio of the call and the stock that is riskless. Solution: (d) (5 points) What is the expected return of the call? Solution: Problem 4 Black Scholes Equation and Brownian Motion. Suppose that the S&P 500 price, St, follows a geometric Brownian motion: dSt = Sedt +oS dB, where u = 8% and o = 20%. For simplicity, assume that there are no dividends. SPXL is an exchange traded fund that uses futures to target a daily return that is three times the S&P 500. Under the assumption of no dividends, the price of SPXL, $t, will follow d = (3u - 2r) Sedt + 30 edB, where r is the continuously compounded risk-free rate. Suppose that r = 2%. Say that currently o = $40 and consider a European call on SPXL expiring in T = 1 year struck at K = $46. (a) (5 points) Compute dy and dfrom Black Scholes equation. Solution: (b) (5 points) Compute the Black Scholes price of the call option. Solution: (c) (5 points) What is the risk-neutral probability the call ends up in the money? You may use any approximation we have talked about in class. Solution: (d) (5 points) Compute the price of a derivative security that pays $1 if the call is in the money at T = 1. Will the expected return of such a derivative be higher or lower than the risk-free rate? Solution: (e) (5 points) Is e-T E[(T - K)+] greater or less than the price of the call? Explain briefly. Solution: (f) (5 points) is the risk-neutral expected return of SPXL higher, lower, or the same as the risk-neutral expected return of the S&P 500? Explain. Solution: (g) (5 points) Now consider a holding period of At = 1/52 (one week). What is the probability that SPXL has a 10% loss in one week according to the geometric Brownian motion assumed in (*)? Solution: (h) (5 points) If the expected return of SPXL was instead just 3 instead of 34 - 2r, would there be an issue? Explain. Solution: Problem 5 Real Options. Suppose that copper price is currently trading at So = $3.50/pound. Futures for delivery of copper in 1 year trade at $3.60/pound. The risk-free rate is 0%. Next year, the price of copper will either rise to $4.20 60% actual probability) or fall to $3.00 (40% actual probability). Copper may or may not have a storage cost and/or convenience yield. (a) (5 points) Compute the risk-neutral probability that copper prices go up. Solution: Suppose that you have an investment project which has the following cash flows: . You have already spent $3M on R&D toward the project. To go forward with the project, you will need an additional investment of $1M at t = 0. At t = 1, you observe the price of copper. After observing the price of copper, if you decide to continue, you must make an additional investment $1M. Additionally, you will be required to purchase 10M pounds of copper. The investment will then produce an immediate cash flow of $35M at t=1. Alternatively, after observing the copper price at t = 1, we can abandon the investment and have no future cash flows. (b) (5 points) Compute the present value of the business strategy which chooses to always invest at both t = 0 and t = 1 and never abandons. Solution: (c) (5 points) Assuming that you invest at t = 0, when will it be optimal for you to choose to abandon the project at t = 1? Solution: (d) (5 points) Would you recommend that we spend the additional $1M at t = 0 to pursue the project? What is the NPV of the optimal strategy? Solution: (e) (5 points) Suppose that you believe that it is very likely that copper prices will rise. Although the market consensus is that there is a 60% chance that copper prices will go up, you believe there is a 90% chance prices will go up. Does that affect the logic you use in making your decision to invest or not? That is, would you be less likely to invest if you believed your costs were likely to high in the future? Explain. Solution: (f) (5 points) Suppose that you believe the project is worth investing in, but would like to hedge your risk. Given an example of a derivative security that you could enter into (specify long or short), that you could use to hedge your risk. Solution