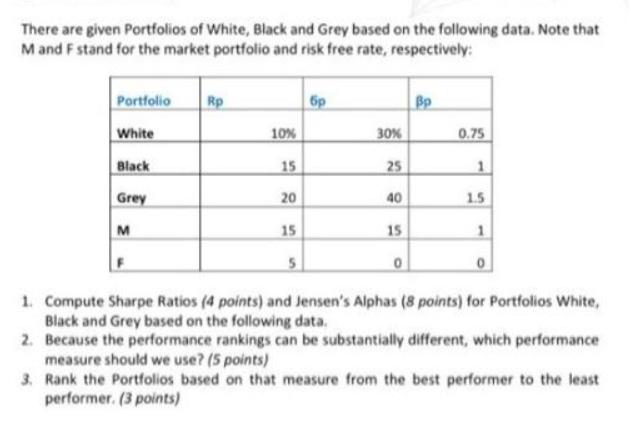
There are given Portfolios of White, Black and Grey based on the following data. Note that M and F stand for the market portfolio and risk free rate, respectively: Portfolio White Black Grey M Rp 10% 15 20 15 5 30% 25 40 15 0 Bp 0.75 1 1.5 1 1. Compute Sharpe Ratios (4 points) and Jensen's Alphas (8 points) for Portfolios White, Black and Grey based on the following data. 2. Because the performance rankings can be substantially different, which performance measure should we use? (5 points) 3. Rank the Portfolios based on that measure from the best performer to the least performer. (3 points) 2 3 4 5 6 7 8 9 SERANGSASANA 10 11 12 13 1) 14 15 16 2) 17 18 19 20:3) 21 22 23 1 2 Portfolio 3 White 4 Black Grey M F 5 6 7 8 9 10 Portfolio White Black Grey M F formula: Sharpe Ratio (Rp-Rf) / Sigma(p) Jensen Alpha Rp - (Rf+beta*(Rm-Rf)) Rp 0.17 0.40 Sharpe Ratio. Jensen Alpha -2.50% 0.00% 10% 15% 20% 15% 5% Rp 0.1 0.15 11 12 13 1) Sharpe Ratio 14 Jensen Alpha 15 0.2 0.15 0.05 Sigma Beta 30% 25% 40% 15% 0% White Black Grey The Sharpe Ratio uses standard deviation as risk factor, which is a measure of total risk i.e. both systematic and unsystematic risk. Whereas Jensen's Alpha uses only beta i.e systematic risk. So, Sharpe ratio is better measure to rank the performance of portfolios. As Black has highest Sharpe ratio it is best performer and White with lowest ratio is least performer among these portfolios. Ranking from best performer to least performer is: Black -> Grey-> White Sharpe Ratio (Rp-Rf) / Sigma(p) Jensen Alpha Rp (Rf+beta"(Rm-Rf)) White (C3-C7)/D3 C3-(C7+E3 (C6-C7)) Sigma 0.3 0.25 0.4 0.15 0 0.75 1 1.5 1 0 0.38 0.00% 0 Beta 0.75 1 1.5 1 Grey Black (C4-C7)/D4 (C5-C7)/D5 C4-(C7+54 (C6-C7)) CS-(C7+E5 (C6-C7)) F G H I L 162) The Sharpe Ratio uses standard deviation as risk factor, which is a measure of total risk Le. both systematic and unsystematic risk. Whereas Jensen's Alpha uses 17 only beta i.e systematic risk. So, Sharpe ratio is better measure to rank the performance of portfolios. 18 19 203) As Black has highest Sharpe ratio it is best performer and White with lowest ratio is least performer among these portfolios. Ranking from best performer to least performer is: Black Grey White 21