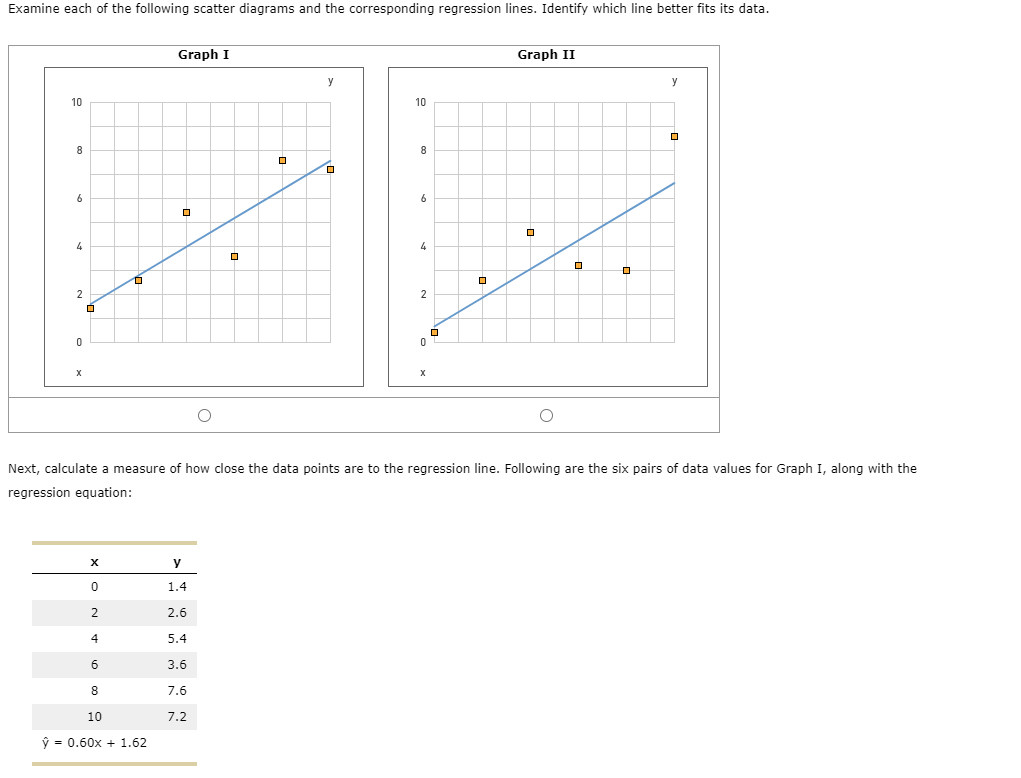
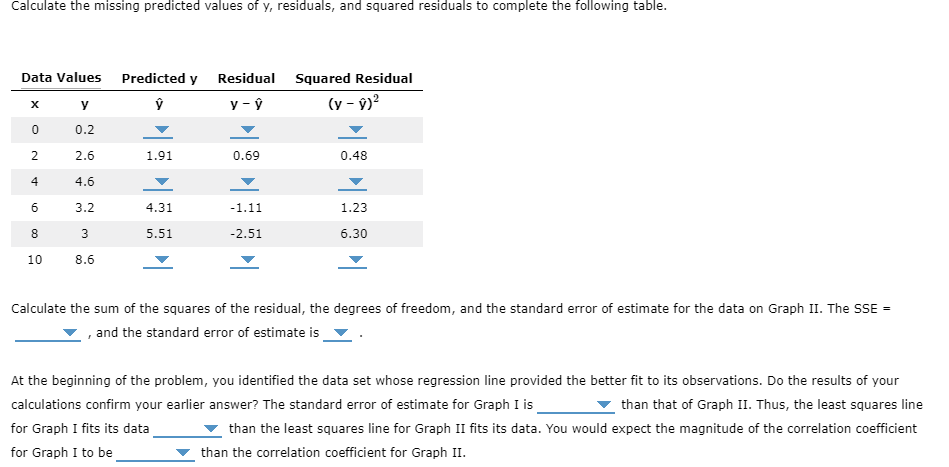
Examine each of the following scatter diagrams and the corresponding regression lines. Identify which line better fits its data. 10 8 6 4 2 0 X 0 2 D 4 Graph I 6 8 10 0.60x + 1.62 0 0 y 1.4 2.6 5.4 3.6 7.6 7.2 10 8 6 4 2 0 0 0 Graph II 0 Next, calculate a measure of how close the data points are to the regression line. Following are the six pairs of data values for Graph I, along with the regression equation: 0 0 y 0 Calculate the missing predicted values of y, residuals, and squared residuals to complete the following table. (Note: Your answers may differ slightly due to rounding. Select the responses that most closely match your results.) Data Values Predicted y Residual y- X 0 2 4 6 8 10 y 1.4 2.6 5.4 3.6 7.6 7.2 X 2.82 4.02 0 2 6.42 4 -0.22 1.38 Calculate the sum of the squares of the residual, the degrees of freedom, and the standard error of estimate for the data on Graph I. The SSE = , and the standard error of estimate is. 6 8 10 = 0.60x + 0.71 1.18 The following are the six pairs of data values for Graph II, along with the regression equation: y 0.2 2.6 4.6 3.2 3 8.6 Squared Residual (y - y)? 0.05 1.90 1.39 Calculate the missing predicted values of y, residuals, and squared residuals to complete the following table. Calculate the missing predicted values of y, residuals, and squared residuals to complete the following table. Data Values Predicted y X 0 2 4 6 8 10 y 0.2 2.6 4.6 3.2 3 8.6 1.91 4.31 5.51 Residual Squared Residual y- (y - 9) 0.69 -1.11 -2.51 0.48 1.23 6.30 Calculate the sum of the squares of the residual, the degrees of freedom, and the standard error of estimate for the data on Graph II. The SSE = , and the standard error of estimate is At the beginning of the problem, you identified the data set whose regression line provided the better fit to its observations. Do the results of your calculations confirm your earlier answer? The standard error of estimate for Graph I is than that of Graph II. Thus, the least squares line for Graph I fits its data than the least squares line for Graph II fits its data. You would expect the magnitude of the correlation coefficient than the correlation coefficient for Graph II. for Graph I to be