Question: F = -kx, (1)w : k/m. (4)1 Ei = 51065.9) We use Eq. (9) to calculate the energy data points {61.51) (t2,E2), ...}, as in


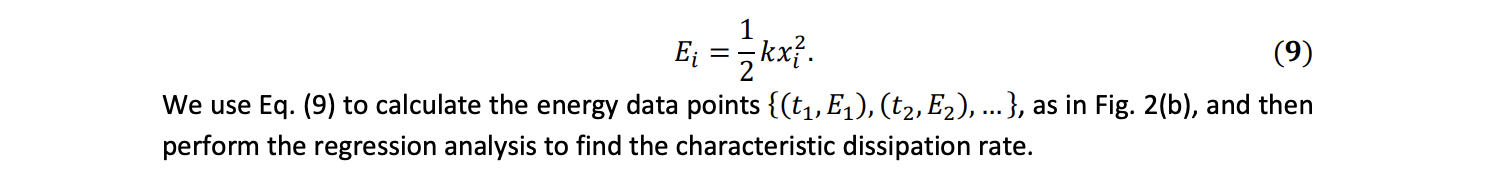


![sig. figs.) [6] 1. Oscillation amplitude A = m 2. Oscillation period](https://s3.amazonaws.com/si.experts.images/answers/2024/07/6687e88574610_9176687e88563cb8.jpg)




![F vs Ax. [4] Answer: \f(3) Analyze the best-fit line. (Express answers](https://s3.amazonaws.com/si.experts.images/answers/2024/07/6687e887261f8_9196687e88705cbb.jpg)
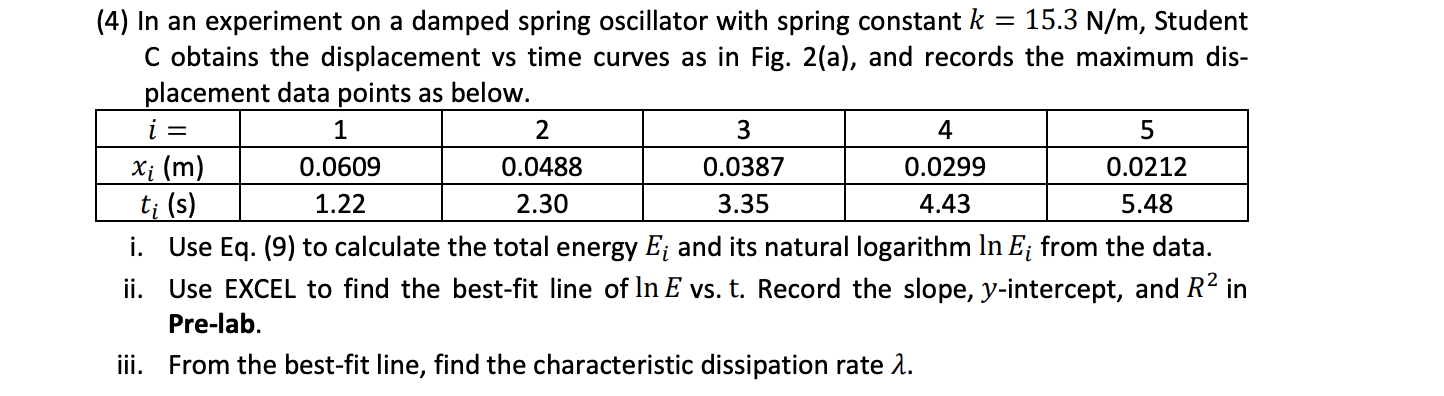
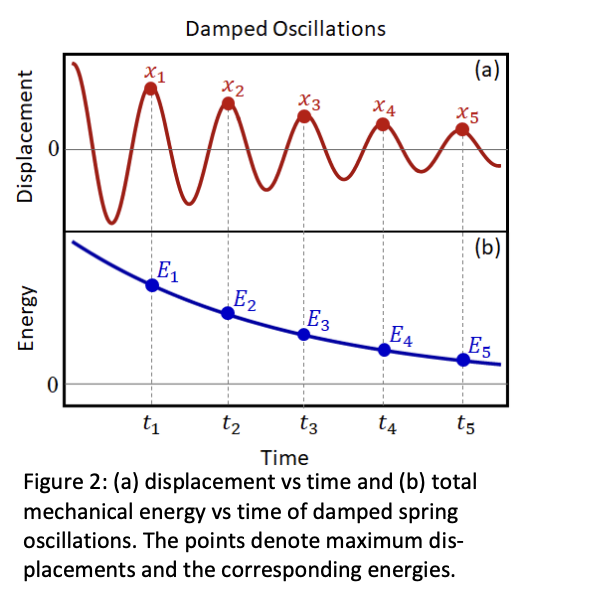
F = -kx, (1)w : k/m. (4)1 Ei = 51065.9) We use Eq. (9) to calculate the energy data points {61.51) (t2,E2), ...}, as in Fig. 2(b), and then perform the regression analysis to find the characteristic dissipation rate. \fDamped Oscillations (a) X4 X5 Displacement 0 (b ) E1 E2 E3 EA E5 Energy O t4 t2 t3 t1 Time Figure 2: (a) displacement vs time and (b) total mechanical energy vs time of damped spring oscillations. The points denote maximum dis- placements and the corresponding energies.(1) Compute the quantities below. (Express answers to 3 sig. figs.) [6] 1. Oscillation amplitude A = m 2. Oscillation period T = S 3. Spring constant k N/m 4. Maximum elastic potential energy U max = L 5. Maximum speed Vmax = m/s 6. Total mechanical energy U (t) + K(t) =_(2) Please discuss how to read out the spring constant k. i. From the best-fit line of F vs Ax. [4] Answer: \f(3) Analyze the best-fit line. (Express answers to 3 sig. figs. whenever applicable) i. (log10 w) = _ X (log10 m) + ; R2 = [9] ii. Spring constant k N/m [1](4) Analyze the damped oscillator. i. Calculate the total energy E; and In E; from the data (remember to use the natural logarithm, which is the function LN in Excel; express answers to 3 sig. figs. whenever applicable) [5] i = 1 2 3 4 5 Ei (J) In Ei ii. Find the best-fit line of In E vs. t. (Express answers to 3 sig. figs.) In E = x t+ ; R2 = [3] iii. Characteristic dissipation rate 1 = _ 1/s [1].(1) In an experiment of a spring oscillator as in Fig. 1, the mass is measured to be m = 0.435 kg, and the displacement as a function of time is measured to be 960?) = 0.313 sin(2.87t + 0.04) with all numbers in SI units. Please find the quantities below. 1. Oscillation amplitude A 4. Maximum elastic potential energy Um: 2. Oscillation period T 5. Maximum speed vmax 3. Spring constant k 6. Total mechanical energy U(t) + K(t) (2) Please discuss how to read out the spring constant A: from the graph of data obtained in the two experiments below. (You will compare both methods in the lab.) i. Student A varies force F exerted on a spring and measures its extension Ax, and plots the best-fit line ofF vs Ax. [Hint: consider Eq. (1).] ii. Student B varies mass m attached on a spring and measures the angular frequency a) of its simple harmonic oscillation, and plots the best-fit line oflog a) vs 10g m. [Hint: consider Eq. (4H (3) From the previous question, Student B records the experimental data in the table below. m (kg) 0.221+0.0005 0.271+0.0005 0.321+0.0005 0.371+0.0005 0.421+0.0005 w (rad/s) 8.44+0.03 7.48+0.02 6.87+0.02 6.53+0.05 5.98+0.03 i. Use EXCEL to find the best-fit line of (log10 w) vs (log10 m). Record the slope, y-intercept, and R2 in Pre-lab. ii. From the best-fit line, find the spring constant k.(4) In an experiment on a damped spring oscillator with spring constant k = 15.3 N/m, Student C obtains the displacement vs time curves as in Fig. 2(a), and records the maximum dis- placement data points as below. i = 1 2 3 4 5 xi (m) 0.0609 0.0488 0.0387 0.0299 0.0212 ti (s) 1.22 2.30 3.35 4.43 5.48 i. Use Eq. (9) to calculate the total energy E; and its natural logarithm In E; from the data. ii. Use EXCEL to find the best-fit line of In E vs. t. Record the slope, y-intercept, and R2 in Pre-lab. iii. From the best-fit line, find the characteristic dissipation rate 1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


