Feedback: #1: This is not the argument in this reading passage. (0/4).

Question 1: Summarize the Riemann sum argument that gives the formula of area as a double integral.

Hint 1: Read the subsection "Areas of Bounded Regions in the Plane" (p. 911 - 913).

Page 911:

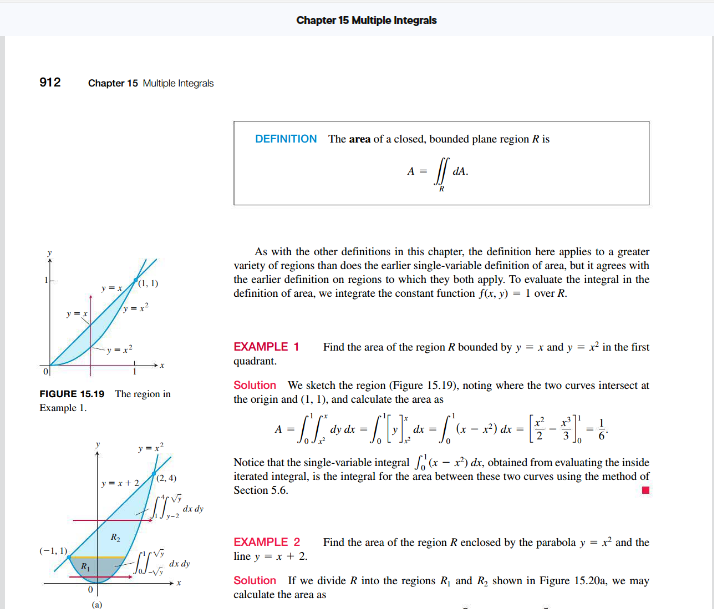
15.3 Area by Double Integration In this section we show how to use double integrals to calculate the areas of bounded regions in the plane, and to find the average value of a function of two variables. Areas of Bounded Regions in the Plane If we take f(x, y) = I in the definition of the double integral over a region R in the precede ing section, the Riemann sums reduce to (1) This is simply the sum of the areas of the small rectangles in the partition of R, and approximates what we would like to call the area of R. As the norm of a partition of R approaches zero, the height and width of all rectangles in the partition approach zero, and the coverage of R becomes increasingly complete (Figure 15.8). We define the area of R to be the limit lim SAA = dA. (2)Chapter 15 Multiple Integrals 912 Chapter 15 Multiple Integrals DEFINITION The area of a closed, bounded plane region R is A = dA. As with the other definitions in this chapter, the definition here applies to a greater variety of regions than does the earlier single-variable definition of area, but it agrees with F= x/ the earlier definition on regions to which they both apply. To evaluate the integral in the definition of area, we integrate the constant function f(x, y) = 1 over R. EXAMPLE 1 Find the area of the region R bounded by y = x and y = x- in the first quadrant. Solution We sketch the region (Figure 15.19), noting where the two curves intersect at FIGURE 15.19 The region in the origin and (1. 1), and calculate the area as Example 1. Notice that the single-variable integral , (x - x7) dx, obtained from evaluating the inside (2, 4) iterated integral, is the integral for the area between these two curves using the method of Section 5.6. faxdy EXAMPLE 2 Find the area of the region R enclosed by the parabola y = a and the (-1, 1) line y = x + 2. Solution If we divide R into the regions R, and Ry shown in Figure 15.20a, we may calculate the area asA = dx dy. On the other hand, reversing the order of integration (Figure 15.20b) gives yux+2 (2, 4) A = dy dx. This second result, which requires only one integral, is simpler to evaluate, giving dy dx (-1, 1) 7x+2 A = dx = / (x + 2 - x) dr = + 2r NIC (b) FIGURE 15.20 Calculating this area EXAMPLE 3 Find the area of the playing field described by takes (a) two double integrals if the first R: -2 = x= 2,-1 - V4- xy= 1+ V4 - x, using integration is with respect to x, but (b) only (a) Fubini's Theorem (b) Simple geometry. one if the first integration is with respect to y (Example 2). Solution The region R is shown in Figure 15.21a.15.3 Area by Double Integration 913 (a) From the symmetries observed in the figure, we see that the area of R is 4 times its area in the first quadrant. As shown in Figure 15.21b. a vertical line at x enters this part of the region at y = 0 and exits at y = 1 + V4 - x. Therefore, using Fubini's Theorem, we have 1+V4-8 dy dx -2 -4/ (1 + V 4 - x ) dx -3 = 4 x + #V4 - x + # sin 1 Integral Table Formula 45 Leaves al = 4(2 + 0 + 2." -0) =8+47. (b) The region R consists of a rectangle mounted on two sides by half disks of radius 2. The area can be computed by summing the area of the 4 % 2 rectangle and the area of a circle of radius 2, so A = 8 + 12- = 8 + 45. 2 Average Value Enters at 0 =4 The average value of an integrable function of one variable on a closed interval is the inte- (b) gral of the function over the interval divided by the length of the interval. For an integrable function of two variables defined on a bounded region in the plane, the average value is the FIGURE 15.21 (a) The playing field integral over the region divided by the area of the region. This can be visualized by thinking described by the region R in Example 3. of the region as being the base of a tank with vertical walls around the boundary of the (b) First quadrant of the playing field. region, and imagining that the tank is filled with water that is sloshing around. The value f(x, y) is then the height of the water that is directly above the point (x, y). The average height of the water in the tank can be found by letting the water settle down to a constant height. This height is equal to the volume of water in the tank divided by the area of R. We therefore define the average value of an integrable function f over a region R as follows:Average value of f over R = f dA. (3) area of R If f is the temperature of a thin plate covering R, then the double integral of f over R divided by the area of K is the plate's average temperature. If f(x, y) is the distance from the point (x, y) to a fixed point P, then the average value of f over R is the average distance of points in R from P. EXAMPLE 4 Find the average value of f(x, y) = x cosxy over the rectangle ROSIST, OSys1. Solution The value of the integral of f over R is Tosaydyax - Asia x cos ay dy = singy + C' (sin x - 0) dr = -cos x =1+1 = 2. JO The area of R is w. The average value of f over R is 2/a