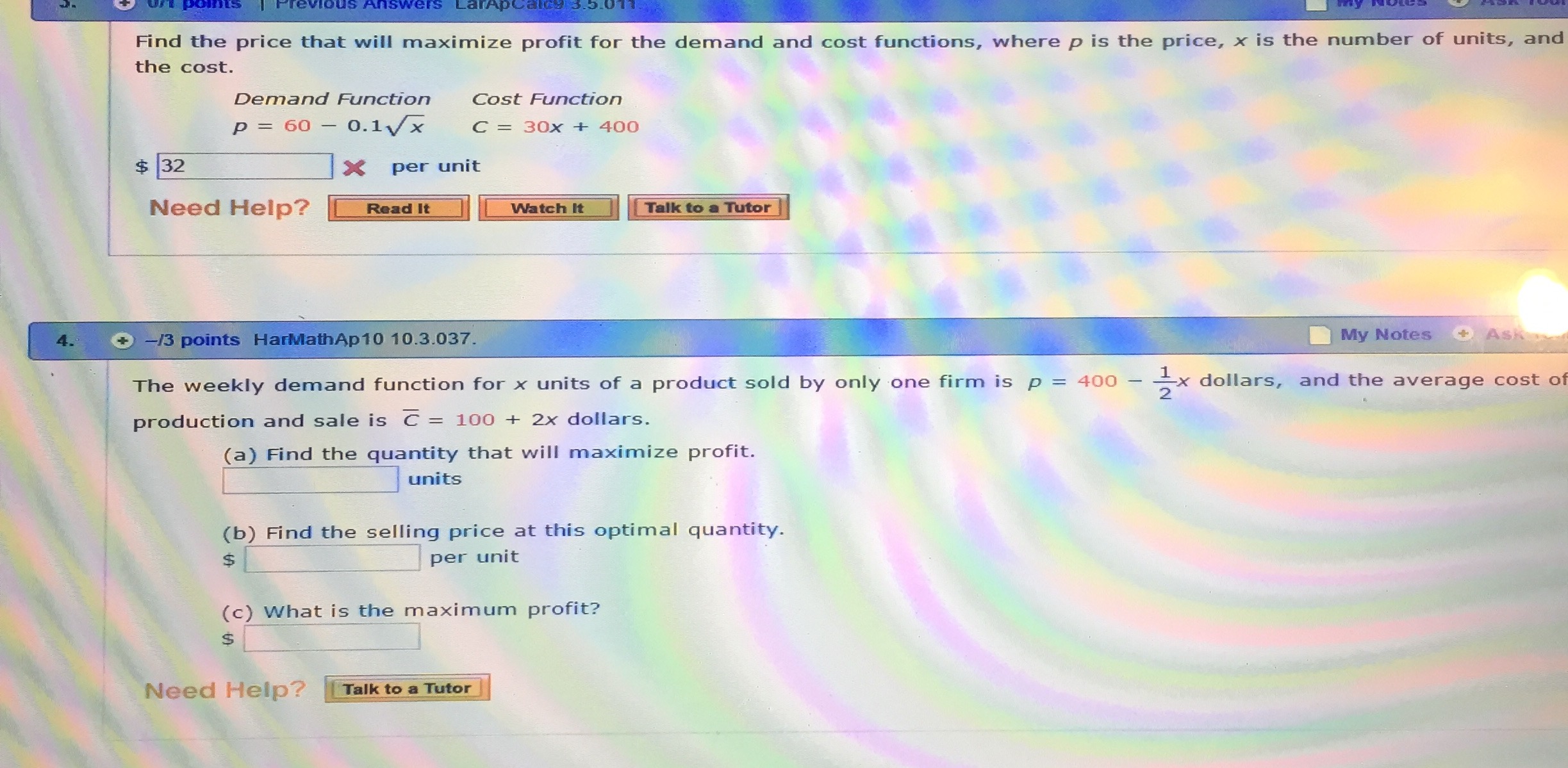
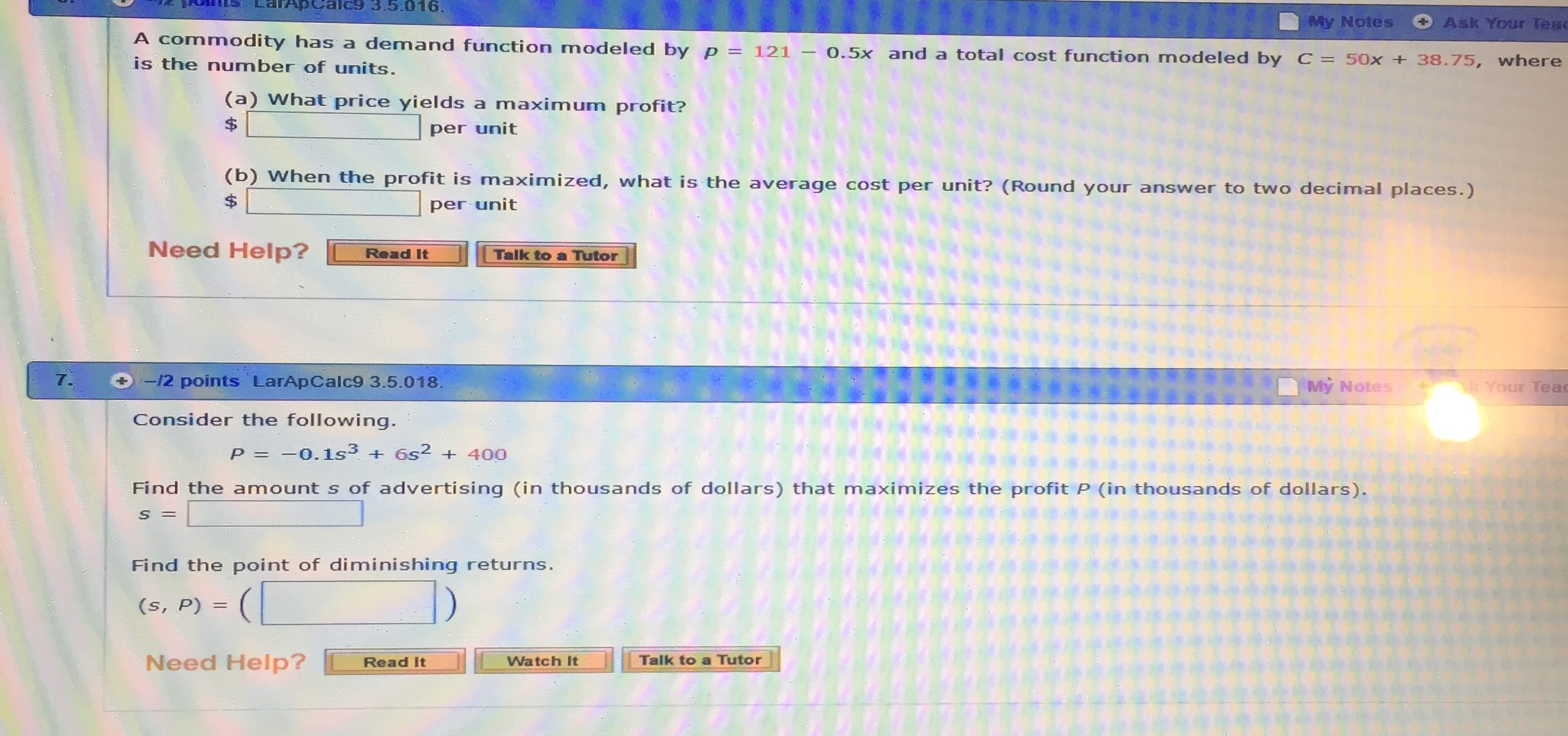
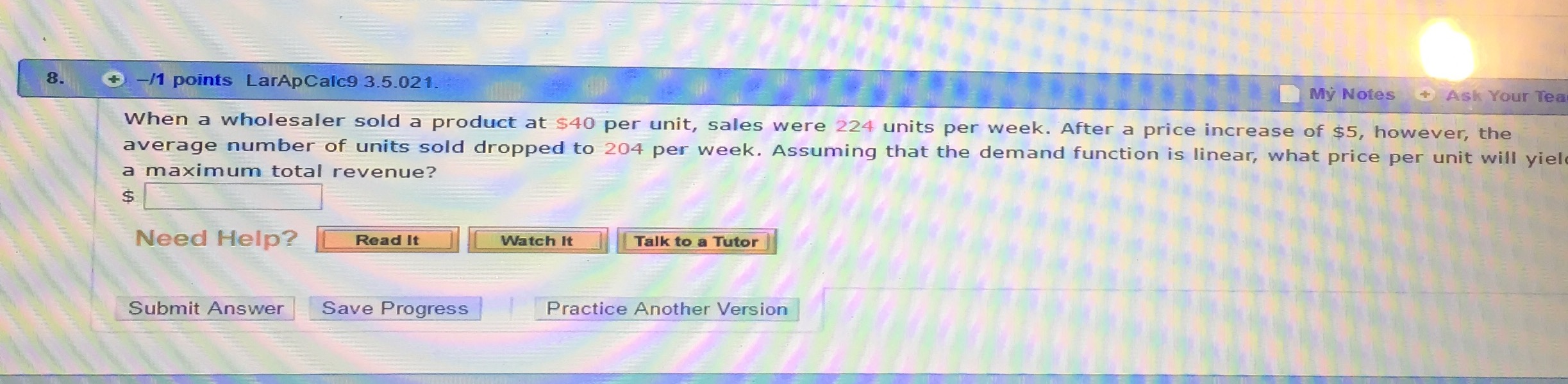
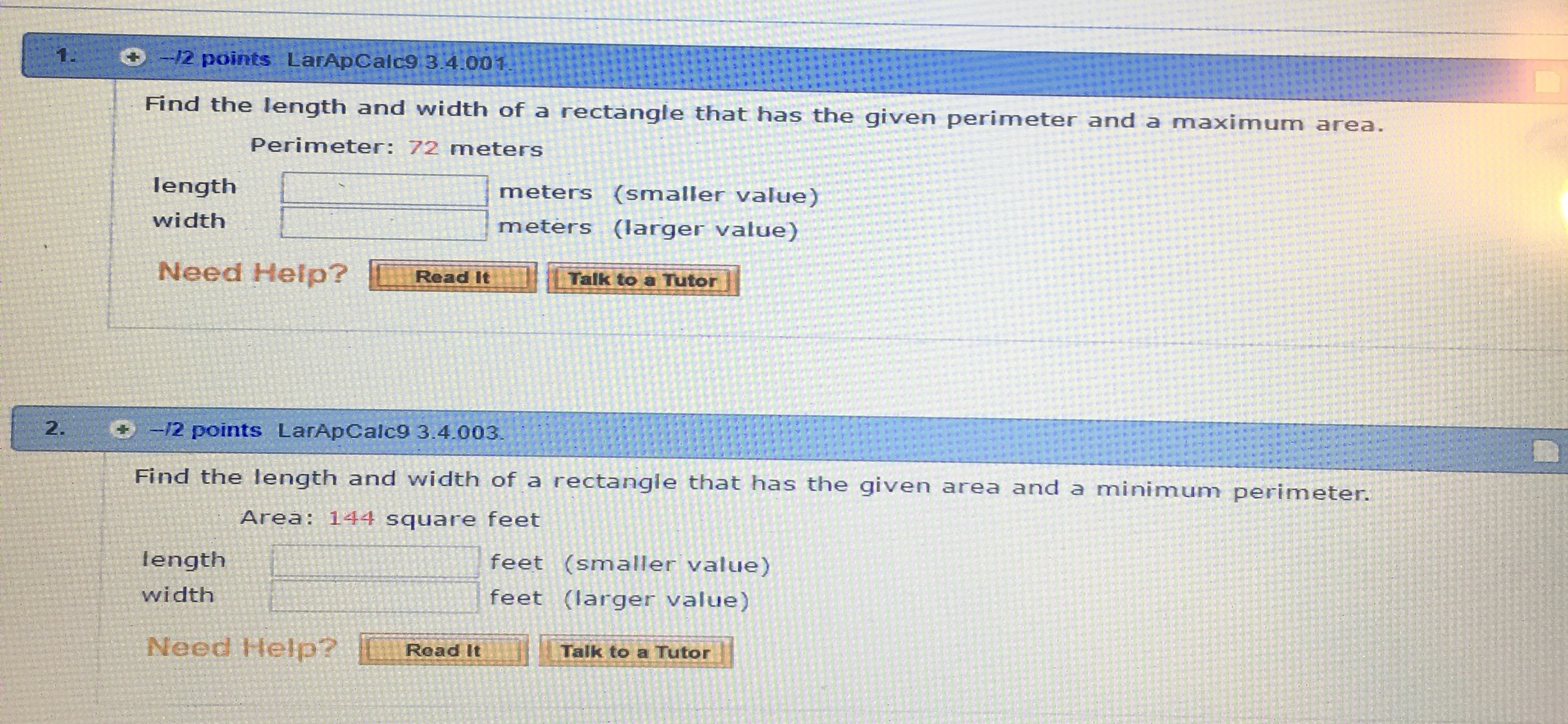
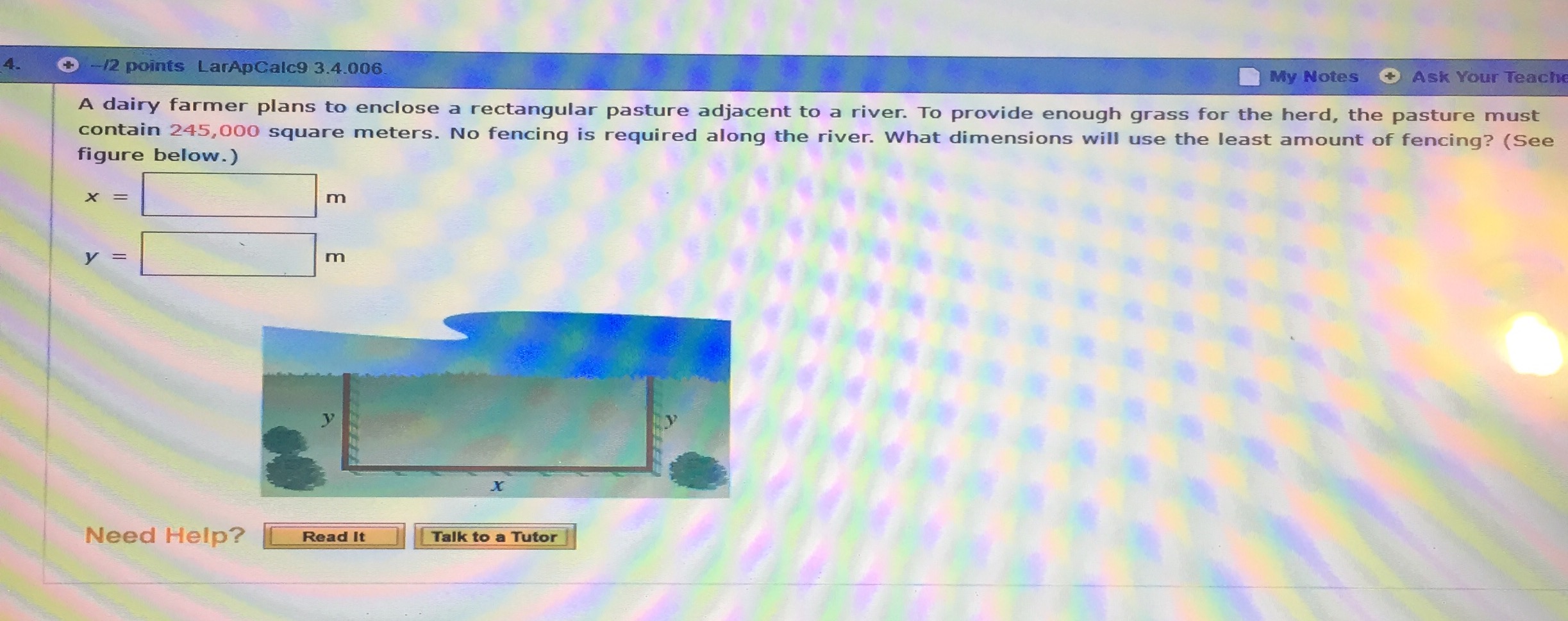
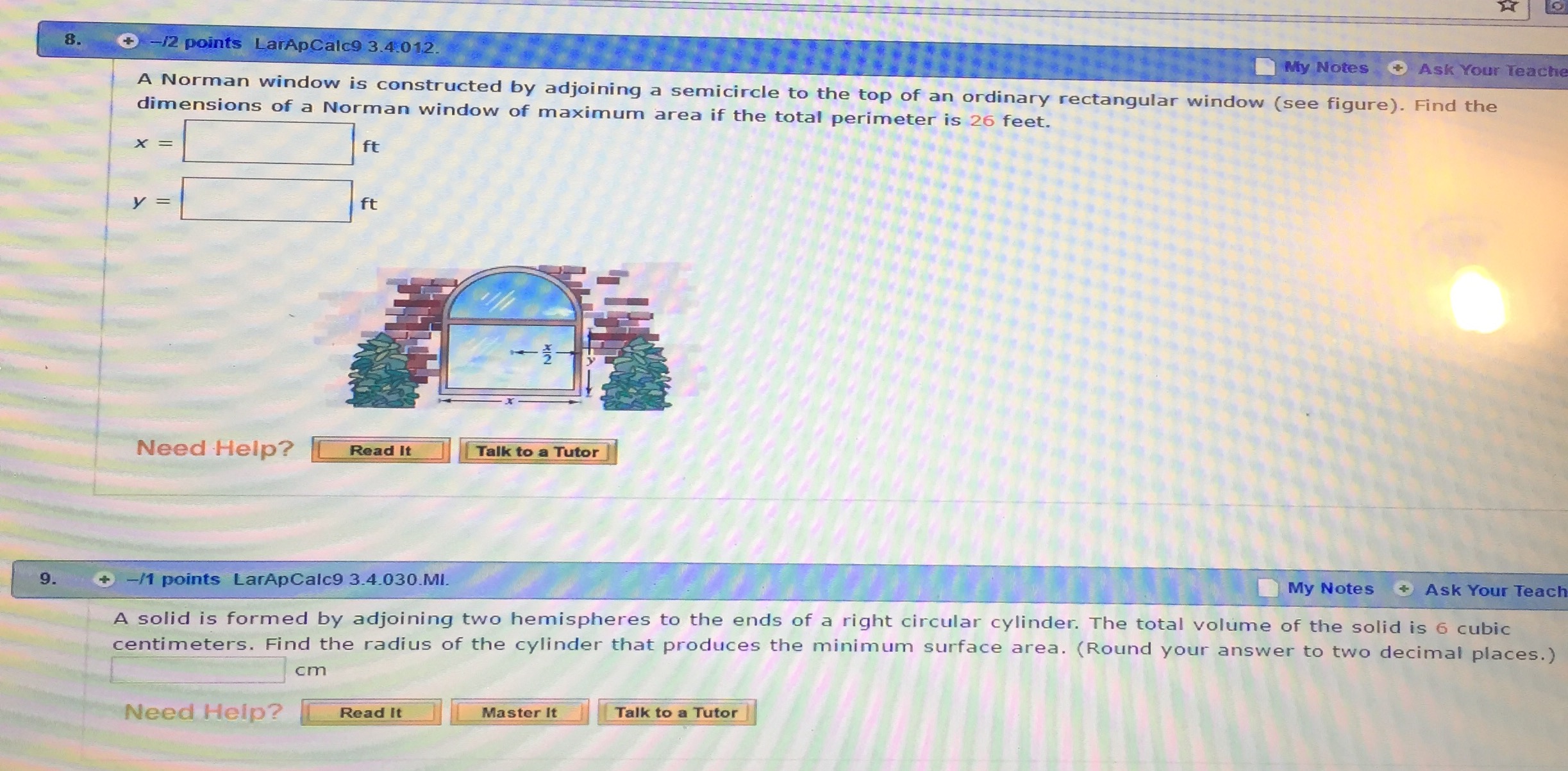
\f\f\f\f\f\f\f\fProblems of Calculus 1. Perimeter : P=72 m length:l=? width: w=? P=2 ( l+w ) P=72 m 2 (l+ w )=72 m l+w= 72m l+ w=36 m w=36 ml 2 Area : A=wl Replacing w in the formula of A A=wl=( 36l ) l A=36 ll 2 To get the maximum area, the first derivative must be equal to zero: 36 ' 2 ' ' 2' A =0 ( 36 ll ) =0 ( 36l ) ( l ) =0 362l =0 36=2 l =l l=18 m 2 Replacing l in the equation of w : w=36 ml=36 m18 m w=18 m The dimensions are: length 18 meters width 18 meters 2. Area : A=144 feet length:l=? 2 width: w=? A=wl A=144 feet 2 wl=144 feet 2 w= 144 feet 2 l Perimeter : P=2 ( l+w ) P=2 l+ 2 w Replacing w in the equation of P: P=2 l+2 w=2l+2 ( 144l ) P=2 l+ 288l 1 To get a minimum perimeter, the first derivative must be equal to zero: ' ' ' P' =0 ( 2l+288 l1 ) =0 ( 2 l )' + ( 288l 1 ) =0 2+288 ( l1) =0 2+288 (1 ) l 11=0 2288 l2=0 2 288 288 288 =0 2= 2 2 l 2=288 l 2 = l 2=144 l 2=144 2 2 l l l=12 feet Replacing l w= in the equation of w : 144 feet 2 144 feet 2 = w=12 feet l 12 feet The dimensions are: length 12 feet width 12 feet 4. Area : A=245,000 m x=? 2 y=? A=bh b=x , h= y A=xy A=245,000m 2 xy=245,000 m2 x= 2 245,000 m y Length of fence :l= y+ x + y l=2 y + x Replacing x in the equation above: 245,000 1 l=2 y + l=2 y +245,000 y y To determine the least amount of fencing, the first derivative must be equal to zero: ' ' ' l ' =0 ( 2 y +245,000 y1 ) =0 ( 2 y )' + ( 245,000 y1) =0 2+245,000 ( y1 ) =0 2+245,000 (1 ) y11=0 2245,000 y2 =0 2 2 2 2 y =245,000 y = 245,000 245,000 =0 2= 2 2 y y 245,000 2 2 y =122,500 y = 122,500 y =350 m 2 Replacing y in the equation of x, we get: 245,000m 2 245,000 m2 x= = x=700 m y 350 m Answer: x= 700 m y= 350 m A rectangular solid with a square base has a surface of 121.5 square centimeters. (Let x represent the length of the sides of the square base and let y represent the height.) (a) Determine the dimensions that yield the maximum volume. 2 Surface Area : S=121.5 cm x=? y=? S=2 wl +2 wh +2lh Width :w=x Length :l=x Height :h= y 2 S=2 xx +2 xy +2 xy S=2 x +4 xy S=121.5 cm2 2 x2 + 4 xy=121.5 cm 2 4 xy=121.5 cm 22 x2 y = 121.5 cm 22 x 2 4x 2 Volume :V =wlh=xxy V =x y Replacing y in the equation of V: 2 2 121.5 cm 2 x V =x 2 =0.25 x ( 121.5 cm 22 x 2 ) V =( 30.375 cm 2 ) x0.5 x 3 4x ( ) To maximize the Volume, the first derivative must be equal to zero: ' ' ' V ' =0 ( 30.375 x0.5 x 3 ) =0 ( 30.375 x )' ( 0.5 x 3 ) =0 30.3750.5 ( x 3 ) =0 30.3750.5 ( 3 x 31 )=0 30.3751.5 x 2=0 30.375=1.5 x2 x2= 20.25 x=4.5 cm Replacing x in the equation of y: 30.375 =x 2 x 2=20.25 1.5 2 2 2 2 2 2 121.5 cm 2 x 121.5 cm 2 ( 4.5 cm) 121.5 cm 2 ( 20.25 cm ) y= = = 4x 18 cm 4 ( 4.5 cm ) 2 y= 2 2 121.5 cm 40.5 cm 81cm = y=4.5 cm 18 cm 18 cm Answer: x= 4.5 cm y=4.5 cm (b) Find the maximum volume. Replacing x and y in the equation of Volume: 2 V =x 2 y=( 4.5 cm ) ( 4.5 cm )=( 20.25 cm2 ) ( 4.5 cm ) V =91.125 cm3 The maximum volume is 91.125 cm3 6. Volume :V =4,913 3 (a) Determine the dimensions that yield the minimum surface area. x=? y=? V =wlh Width :w=x Length :l=x Height :h= y 2 V =xxy V =x y V =4,913 3 x 2 y=4913 3 y= 4,913 2 x 3 Surface Area : S=2 wl+2 wh+2 lh=2 xx +2 xy+ 2 xy S=2 x 2 + 4 xy Replacing y in the equation of Surface Area: 4,913 19,652 S=2 x 2+ 4 x =2 x2 + S=2 x 2 +19,652 x 1 2 x x ( ) To minimize the Surface area, the first derivative must be equal to zero: ' ' ' ' ' S ' =0 ( 2 x 2 +19,652 x 1 ) =0 ( 2 x 2 ) + ( 19,652 x 1 ) =0 2 ( x 2 ) +19,652 ( x 1 ) =0 2 ( 2 x 21 ) +19,652 (1 ) x 11=0 4 x19,652 x2=0 4 x 4 x ( x 2 )=19,652 4 x 3=19,652 x 3= 19,652 19,652 =0 4 x= 2 x x2 19,652 3 x 3=4,913 x3 =3 4,913 x=17 4 Replacing x in the equation of y: 17 2 4,913 3 4,913 3 y= = x2 The dimensions that yield the minimum surface area are: x= 17 in y=17 in (b) Find the minimum surface area. Replacing x and y in the equation of Surface area: 17 17 17 2 S=2 x + 4 xy=2 S=1,734 2 The minimum surface area is: 1,734 in2 8. Total Perimeter : PT =26 ft x=? y=? PT =b+h+ h+ Psc P T =b+2 h+ Psc 1 Perimeter of the semicircle : Psc = d Psc = d 2 2 Diameter : d=x Psc = d Psc = x 2 2 b=x , h= y Replacing b, h and Psc in the equation of PT: 2+ PT =b+2 h+ Psc =x +2 y+ x=2 y + 1+ x PT =2 y + x 2 2 2 ( ) ( ) ( 2+2 ) x =26 ft 2 y=26 ft( 2+2 ) x y = 262ft ( 2+22 ) x 2+ y=13 ft( x 4 ) P=26 ft 2 y+ Total Area : AT = Ar + A sc Area of therectangle : Ar =bh A r=xy Area of the semicircle : A sc = 1 2 2 d = d A sc= x 2 2 4 8 8 ( ) Replacing Ar and Asc in the formula of AT: A T =A r + A sc A T = xy+ x 2 8 Replacing y in the equation of AT: 2+ 2+ 2 2 A T =xy + x 2=x 13 x + x 2=13 x x+ x 8 4 8 4 8 [ ( )] A T =13 x+ ( ) ( 8 2+4 ) x =13 x +( 28( 2+ ) ) x =13 x+( 42 )x 8 2 2 2 A T =13 x+ 4+ x A =13 x( x ( 4 8 ) 8 ) 2 2 T To maximize the total area, the first derivative must be equal to zero: ' ' 4 + 2 4+ 2 4 + 2 ' ' ' A T =0 13 x x =0 ( 13 x ) x =0 13 ( x ) =0 8 8 8 [ ( )] 13 x= ( 4+8 )2 x 21 [( ) ] ( ) 52 =x x= ft ( 4 +4 ) x=0 13=( 4+4 ) x 134 4+ 4+ =0 13 52 52 = =7.281288996 x 7.28 ft 4+ 3.141592654 7.141592654 Replacing x in the equation of y: 13 ( 2+ ) 2+ 2+ 52 y=13 ft x=13 ft ft =13 ft ft 4 4 4+ 4+ ( ) ( )( y= 13 [ 4 + ( 2+ ) ] 13 ( 4+ )13 ( 2+ ) 13 ( 4+ 2 ) 13 ( 2 ) ft = ft= ft= ft 4 + 4+ 4+ 4+ y= 26 ft 4+ y= 26 26 ft= ft y =3.640644498 ft y 3.64 ft 4 +3.141592654 7.141592654 x= 7.28 ft y=3.64 ft 9. ) Total Volume :V T =6 cm 3 r=? V T =2V h +V c Volume of each hemisphere :V h 2 Volume of the cylinder :V c = r h Volume of a sphere :V s= V s=2V h = 4 3 r 3 4 3 r 3 4 3 Replacing 2V h=V s = 3 r and V T =2V h +V c =V s +V c V T = V T =6 cm3 V c = r 2 h VT in the equation of 4 3 r + r2 h 3 4 3 4 3 6 cm3 4 3 r + r 2 h=6 cm 3 r 2 h=6 cm3 r h= r 2 3 3 r 3 r2 6 4 h= r 2 cm3 r 3 Total Surface Area: ST =2 S h + Sc Surface area of each hemisphere : S h Surface area of the cylinder :S c =2 rh Surface area of a sphere :S s=4 r 2 S s =2 Sh =4 r 2 2 Replacing 2 S h=Ss =4 r and S c =2 rh in the equation of ST : S T =2 S h+ S c =S s + Sc ST =4 r 2+2 rh Replacing h in the equation above: 6 4 8 2 S T =4 r 2 +2 r r 2 r =4 r 2 +12r 1 r 3 3 ( ( S T =12r 1 + 4 S T =12r 1 + ) 3 ( 4 )8 2 8 2 12 8 2 r =12 r 1 + r =12 r1+ r 3 3 3 ( ) ) ( ) 4 2 r 3 To minimize the surface area, the first derivative must be equal to zero: ' ' 4 ' 4 2 ' 4 2 ' ( r 2 ) =0 S 'T =0 12 r1+ r =0 ( 12 r1 ) + r =0 12 ( r 1 ) + 3 3 3 ( 12 (1 ) r11 + ) ( ) 4 ( 2 r 21 ) =0 12 r2+ 8 r =0 122 + 8 r=0 8 r= 122 3 3 3 3 r r r r 2= r= 3 3 (12 ) 3 9 3 9 3 9 r3 = r 3 = r = cm 8 2 2 2 9 3 9 3 cm= cm= 1.432394488 cm=1.127251652 cm 6.283185307 2 ( 3.141592654 ) r 1.13 cm The radius of the cylinder that produces the minimum surface area is 1.13 cm Price: p=? 3. Demand function : p=600.1 x Cost function :C=30 x +400 Revenue : R= px p in the equation of R: Replacing 1 2 R= px=( 600.1 x ) x=(600.1 x ) x=60 x0.1 x R=60 x0.1 x 1+2 2 R=60 x 0.1 x 1 +1 2 =60 x0.1 x 1 +2( 1) 2 3 2 Profit : P=RC Replacing R and C in the equation of P: 3 2 3 2 P=RC=( 60 x0.1 x )( 30 x + 400 )=60 x0.1 x 30 x400 3 2 P=30 x0.1 x 400 To maximize profit, the first derivative must be equal to zero: ' 3 2 3 ' 2 3 ' 2 P =0 ( 30 x0.1 x 400 ) =0 (30 x ) (0.1 x ) ( 400 ) =0 300.1 ( x ) 0=0 ' 300.1 ( 3 ' ) 3 21 x =0 300.15 x 2 1 2 1 1 32 ( 1) 2 =0 300.15 x ' 32 2 1 =0 300.15 x 2 =0 1 2 ( ) 30 30=0.15 x =x 2 x 2 =200 x 2 = ( 200 )2 x=40,000 0.15 Replacing x in the equation of p: x=40,000 p=600.1 x=600.1 40,000=600.1 ( 200 )=6020 p=40 The price that will maximize profit is $40 per unit 4. 1 Demand function : p=400 x 2 Average cost of productionsale: C=100+ 2x Revenue : R= px Replacing p in the equation of R: 1 1 R= px= 400 x x R=400 x x 2 2 2 ( ) Cost function :C=C x Replacing C in the equation of C: x=( 100+2 x ) x C=100 x+ 2 x 2 C=C Profit : P=RC Replacing R and C in the equation of P: 1 1 P=RC= 400 x x2 ( 100 x +2 x 2 ) =400 x x 2100 x 2 x 2 2 2 ( ) 1+2 ( 2 ) 1 1+4 5 P=300 x( +2 ) x =300 x( x =300 x( x P=300 x x 2 2 ) 2 ) 2 2 2 2 2 To maximize profit, the first derivative must be equal to zero: ' ' ' 5 ' 5 5 5 P' =0 300 x x 2 =0 ( 300 x ) x 2 =0 300 ( x 2 ) =0 300 ( 2 x )=0 2 2 2 2 ( ) 3005 x=0 300=5 x ( ) 300 =x x=60 5 Replacing x in the equation of p: 1 1 x=60 p=400 x=400 ( 60 )=40030 p=370 2 2 Replacing x in the equation of P: 5 5 5 x=60 P=300 x x2 =300 (60 ) ( 60 )2=18,000 ( 3,600 )=18,0009,000 2 2 2 P=9,000 (a) 60 units (b) $ 370 per unit (c) $ 9,000 6. Demand function : p=1210.5 x Cost function :C=50 x +38.75 Revenue : R= px Replacing p in the equation of R: R= px=( 1210.5 x ) x R=121 x0.5 x 2 Profit : P=RC Replacing R and C in the equation of P: P=RC=( 121 x 0.5 x 2 ) ( 50 x +38.75 ) =121 x0.5 x 250 x38.75 2 P=71 x0.5 x 38.75 To maximize the profit P, the first derivative must be equal to zero: ' ' P' =0 ( 71 x0.5 x 238.75 ) =0 ( 71 x )' ( 0.5 x 2 ) ( 38.75 )' =0 ' 710.5 ( x 2 ) 0=0 710.5 ( 2 x )=0 71x=0 x=71 Replacing x in the equation of p: x=71 p=1210.5 x=1210.5 ( 71 )=12135.5 p=85.5 Replacing x in the equation of C: x=71 C=50 x+ 38.75=50 ( 71 )+ 38.75=3,550+38.75 C=3,588.75 C = 3,588.75 C=50.54577464 Average cost : C= C 50.55 x 71 (a) $ 85.5 per unit (b) $ 50.55 per unit 3 2 P=0.1 s + 6 s + 400 7. To maximize the profit P, the first derivative must be equal to zero: ' ' ' P' =0 P' = (0.1 s3 +6 s2 + 400 ) =0 P' =( 0.1 s3 ) + ( 6 s2 ) + ( 400 )' =0 ' 3 ' 2 ' ' 2 ' 2 P =0.1 ( s ) +6 ( s ) +0=0 P =0.1 ( 3 s ) +6 ( 2 s )=0 P =0.3 s +12 s=0 P' =s (0.3 s+12 ) =0 { s 1=0, It is not a solution 12 0.3 s+12=0 12=0.3 s =s s 2=40 0.3 The amount of advertising that maximizes the profit is s=40 To find the point of diminishing returns, the second derivative of the profit must be equal to zero: ' ' ' ' P' ' =0 ( P' ) =0 (0.3 s 2+12 s ) =0 ( 0.3 s 2 ) + (12 s )' =0 0.3 ( s 2 ) +12=0 0.3 ( 2 s ) +12=0 0.6 s +12=0 12=0.6 s 12 =s s=20 0.6 Replacing s in the equation of P: 3 2 3 2 s=20 P=0.1 s + 6 s + 400=0.1 ( 20 ) +6 ( 20 ) +400=0.1 ( 8,000 )+ 6 ( 400 ) + 400 P=800+2,400+ 400 P=2,000 The point of diminishing returns is 8. ( s , P ) =( 20,2,000 ) p1=40 x 1=224 p2= p1 +5=40+5 p2 =45 x 2=204 Assuming that the demand function p is linear: p p1=m ( xx 1 ) Slope : m= p 2 p1 4540 5 = = m=0.25 x 2x 1 204224 20 Replacing m in the demand function p: p p1=m ( xx 1 ) p40=0.25 ( x224 ) p40=0.25 x +56 p=0.25 x+ 56+40 p=0.25 x+ 96 Revenue : R= px Replacing p in the equation of R: R= px=(0.25 x+ 96 ) x R=0.25 x2 + 96 x To get the maximum Revenue R, the first derivative must be equal to zero: ' ' ' R' =0 (0.25 x 2 +96 x ) =0 ( 0.25 x 2 ) + ( 96 x )' =0 0.25 ( x 2 ) + 96=0 0.25 ( 2 x )+ 96=0 0.5 x+ 96=0 96=0.5 x 96 =x x=192 0.5 Replacing x in the equation of p: x=192 p=0.25 x +96=0.25 ( 192 ) +96=48+ 96 p=48 The price per unit will yield a maximum total revenue is $ 48. Problems of Calculus 1. Perimeter : P=72 m length:l=? width: w=? P=2 ( l+w ) P=72 m 2 (l+ w )=72 m l+w= 72m l+ w=36 m w=36 ml 2 Area : A=wl Replacing w in the formula of A A=wl=( 36l ) l A=36 ll 2 To get the maximum area, the first derivative must be equal to zero: 36 ' 2 ' ' 2' A =0 ( 36 ll ) =0 ( 36l ) ( l ) =0 362l =0 36=2 l =l l=18 m 2 Replacing l in the equation of w : w=36 ml=36 m18 m w=18 m The dimensions are: length 18 meters width 18 meters 2. Area : A=144 feet length:l=? 2 width: w=? A=wl A=144 feet 2 wl=144 feet 2 w= 144 feet 2 l Perimeter : P=2 ( l+w ) P=2 l+ 2 w Replacing w in the equation of P: P=2 l+2 w=2l+2 ( 144l ) P=2 l+ 288l 1 To get a minimum perimeter, the first derivative must be equal to zero: ' ' ' P' =0 ( 2l+288 l1 ) =0 ( 2 l )' + ( 288l 1 ) =0 2+288 ( l1) =0 2+288 (1 ) l 11=0 2288 l2=0 2 288 288 288 =0 2= 2 2 l 2=288 l 2 = l 2=144 l 2=144 2 2 l l l=12 feet Replacing l w= in the equation of w : 144 feet 2 144 feet 2 = w=12 feet l 12 feet The dimensions are: length 12 feet width 12 feet 4. Area : A=245,000 m x=? 2 y=? A=bh b=x , h= y A=xy A=245,000m 2 xy=245,000 m2 x= 2 245,000 m y Length of fence :l= y+ x + y l=2 y + x Replacing x in the equation above: 245,000 1 l=2 y + l=2 y +245,000 y y To determine the least amount of fencing, the first derivative must be equal to zero: ' ' ' l ' =0 ( 2 y +245,000 y1 ) =0 ( 2 y )' + ( 245,000 y1) =0 2+245,000 ( y1 ) =0 2+245,000 (1 ) y11=0 2245,000 y2 =0 2 2 2 2 y =245,000 y = 245,000 245,000 =0 2= 2 2 y y 245,000 2 2 y =122,500 y = 122,500 y =350 m 2 Replacing y in the equation of x, we get: 245,000m 2 245,000 m2 x= = x=700 m y 350 m Answer: x= 700 m y= 350 m A rectangular solid with a square base has a surface of 121.5 square centimeters. (Let x represent the length of the sides of the square base and let y represent the height.) (a) Determine the dimensions that yield the maximum volume. 2 Surface Area : S=121.5 cm x=? y=? S=2 wl +2 wh +2lh Width :w=x Length :l=x Height :h= y 2 S=2 xx +2 xy +2 xy S=2 x +4 xy S=121.5 cm2 2 x2 + 4 xy=121.5 cm 2 4 xy=121.5 cm 22 x2 y = 121.5 cm 22 x 2 4x 2 Volume :V =wlh=xxy V =x y Replacing y in the equation of V: 2 2 121.5 cm 2 x V =x 2 =0.25 x ( 121.5 cm 22 x 2 ) V =( 30.375 cm 2 ) x0.5 x 3 4x ( ) To maximize the Volume, the first derivative must be equal to zero: ' ' ' V ' =0 ( 30.375 x0.5 x 3 ) =0 ( 30.375 x )' ( 0.5 x 3 ) =0 30.3750.5 ( x 3 ) =0 30.3750.5 ( 3 x 31 )=0 30.3751.5 x 2=0 30.375=1.5 x2 x2= 20.25 x=4.5 cm Replacing x in the equation of y: 30.375 =x 2 x 2=20.25 1.5 2 2 2 2 2 2 121.5 cm 2 x 121.5 cm 2 ( 4.5 cm) 121.5 cm 2 ( 20.25 cm ) y= = = 4x 18 cm 4 ( 4.5 cm ) 2 y= 2 2 121.5 cm 40.5 cm 81cm = y=4.5 cm 18 cm 18 cm Answer: x= 4.5 cm y=4.5 cm (b) Find the maximum volume. Replacing x and y in the equation of Volume: 2 V =x 2 y=( 4.5 cm ) ( 4.5 cm )=( 20.25 cm2 ) ( 4.5 cm ) V =91.125 cm3 The maximum volume is 91.125 cm3 6. Volume :V =4,913 3 (a) Determine the dimensions that yield the minimum surface area. x=? y=? V =wlh Width :w=x Length :l=x Height :h= y 2 V =xxy V =x y V =4,913 3 x 2 y=4913 3 y= 4,913 2 x 3 Surface Area : S=2 wl+2 wh+2 lh=2 xx +2 xy+ 2 xy S=2 x 2 + 4 xy Replacing y in the equation of Surface Area: 4,913 19,652 S=2 x 2+ 4 x =2 x2 + S=2 x 2 +19,652 x 1 2 x x ( ) To minimize the Surface area, the first derivative must be equal to zero: ' ' ' ' ' S ' =0 ( 2 x 2 +19,652 x 1 ) =0 ( 2 x 2 ) + ( 19,652 x 1 ) =0 2 ( x 2 ) +19,652 ( x 1 ) =0 2 ( 2 x 21 ) +19,652 (1 ) x 11=0 4 x19,652 x2=0 4 x 4 x ( x 2 )=19,652 4 x 3=19,652 x 3= 19,652 19,652 =0 4 x= 2 x x2 19,652 3 x 3=4,913 x3 =3 4,913 x=17 4 Replacing x in the equation of y: 17 2 4,913 3 4,913 3 y= = x2 The dimensions that yield the minimum surface area are: x= 17 in y=17 in (b) Find the minimum surface area. Replacing x and y in the equation of Surface area: 17 17 17 2 S=2 x + 4 xy=2 S=1,734 2 The minimum surface area is: 1,734 in2 8. Total Perimeter : PT =26 ft x=? y=? PT =b+h+ h+ Psc P T =b+2 h+ Psc 1 Perimeter of the semicircle : Psc = d Psc = d 2 2 Diameter : d=x Psc = d Psc = x 2 2 b=x , h= y Replacing b, h and Psc in the equation of PT: 2+ PT =b+2 h+ Psc =x +2 y+ x=2 y + 1+ x PT =2 y + x 2 2 2 ( ) ( ) ( 2+2 ) x =26 ft 2 y=26 ft( 2+2 ) x y = 262ft ( 2+22 ) x 2+ y=13 ft( x 4 ) P=26 ft 2 y+ Total Area : AT = Ar + A sc Area of therectangle : Ar =bh A r=xy Area of the semicircle : A sc = 1 2 2 d = d A sc= x 2 2 4 8 8 ( ) Replacing Ar and Asc in the formula of AT: A T =A r + A sc A T = xy+ x 2 8 Replacing y in the equation of AT: 2+ 2+ 2 2 A T =xy + x 2=x 13 x + x 2=13 x x+ x 8 4 8 4 8 [ ( )] A T =13 x+ ( ) ( 8 2+4 ) x =13 x +( 28( 2+ ) ) x =13 x+( 42 )x 8 2 2 2 A T =13 x+ 4+ x A =13 x( x ( 4 8 ) 8 ) 2 2 T To maximize the total area, the first derivative must be equal to zero: ' ' 4 + 2 4+ 2 4 + 2 ' ' ' A T =0 13 x x =0 ( 13 x ) x =0 13 ( x ) =0 8 8 8 [ ( )] 13 x= ( 4+8 )2 x 21 [( ) ] ( ) 52 =x x= ft ( 4 +4 ) x=0 13=( 4+4 ) x 134 4+ 4+ =0 13 52 52 = =7.281288996 x 7.28 ft 4+ 3.141592654 7.141592654 Replacing x in the equation of y: 13 ( 2+ ) 2+ 2+ 52 y=13 ft x=13 ft ft =13 ft ft 4 4 4+ 4+ ( ) ( )( y= 13 [ 4 + ( 2+ ) ] 13 ( 4+ )13 ( 2+ ) 13 ( 4+ 2 ) 13 ( 2 ) ft = ft= ft= ft 4 + 4+ 4+ 4+ y= 26 ft 4+ y= 26 26 ft= ft y =3.640644498 ft y 3.64 ft 4 +3.141592654 7.141592654 x= 7.28 ft y=3.64 ft 9. ) Total Volume :V T =6 cm 3 r=? V T =2V h +V c Volume of each hemisphere :V h 2 Volume of the cylinder :V c = r h Volume of a sphere :V s= V s=2V h = 4 3 r 3 4 3 r 3 4 3 Replacing 2V h=V s = 3 r and V T =2V h +V c =V s +V c V T = V T =6 cm3 V c = r 2 h VT in the equation of 4 3 r + r2 h 3 4 3 4 3 6 cm3 4 3 r + r 2 h=6 cm 3 r 2 h=6 cm3 r h= r 2 3 3 r 3 r2 6 4 h= r 2 cm3 r 3 Total Surface Area: ST =2 S h + Sc Surface area of each hemisphere : S h Surface area of the cylinder :S c =2 rh Surface area of a sphere :S s=4 r 2 S s =2 Sh =4 r 2 2 Replacing 2 S h=Ss =4 r and S c =2 rh in the equation of ST : S T =2 S h+ S c =S s + Sc ST =4 r 2+2 rh Replacing h in the equation above: 6 4 8 2 S T =4 r 2 +2 r r 2 r =4 r 2 +12r 1 r 3 3 ( ( S T =12r 1 + 4 S T =12r 1 + ) 3 ( 4 )8 2 8 2 12 8 2 r =12 r 1 + r =12 r1+ r 3 3 3 ( ) ) ( ) 4 2 r 3 To minimize the surface area, the first derivative must be equal to zero: ' ' 4 ' 4 2 ' 4 2 ' ( r 2 ) =0 S 'T =0 12 r1+ r =0 ( 12 r1 ) + r =0 12 ( r 1 ) + 3 3 3 ( 12 (1 ) r11 + ) ( ) 4 ( 2 r 21 ) =0 12 r2+ 8 r =0 122 + 8 r=0 8 r= 122 3 3 3 3 r r r r 2= r= 3 3 (12 ) 3 9 3 9 3 9 r3 = r 3 = r = cm 8 2 2 2 9 3 9 3 cm= cm= 1.432394488 cm=1.127251652 cm 6.283185307 2 ( 3.141592654 ) r 1.13 cm The radius of the cylinder that produces the minimum surface area is 1.13 cm Price: p=? 3. Demand function : p=600.1 x Cost function :C=30 x +400 Revenue : R= px p in the equation of R: Replacing 1 2 R= px=( 600.1 x ) x=(600.1 x ) x=60 x0.1 x R=60 x0.1 x 1+2 2 R=60 x 0.1 x 1 +1 2 =60 x0.1 x 1 +2( 1) 2 3 2 Profit : P=RC Replacing R and C in the equation of P: 3 2 3 2 P=RC=( 60 x0.1 x )( 30 x + 400 )=60 x0.1 x 30 x400 3 2 P=30 x0.1 x 400 To maximize profit, the first derivative must be equal to zero: ' 3 2 3 ' 2 3 ' 2 P =0 ( 30 x0.1 x 400 ) =0 (30 x ) (0.1 x ) ( 400 ) =0 300.1 ( x ) 0=0 ' 300.1 ( 3 ' ) 3 21 x =0 300.15 x 2 1 2 1 1 32 ( 1) 2 =0 300.15 x ' 32 2 1 =0 300.15 x 2 =0 1 2 ( ) 30 30=0.15 x =x 2 x 2 =200 x 2 = ( 200 )2 x=40,000 0.15 Replacing x in the equation of p: x=40,000 p=600.1 x=600.1 40,000=600.1 ( 200 )=6020 p=40 The price that will maximize profit is $40 per unit 4. 1 Demand function : p=400 x 2 Average cost of productionsale: C=100+ 2x Revenue : R= px Replacing p in the equation of R: 1 1 R= px= 400 x x R=400 x x 2 2 2 ( ) Cost function :C=C x Replacing C in the equation of C: x=( 100+2 x ) x C=100 x+ 2 x 2 C=C Profit : P=RC Replacing R and C in the equation of P: 1 1 P=RC= 400 x x2 ( 100 x +2 x 2 ) =400 x x 2100 x 2 x 2 2 2 ( ) 1+2 ( 2 ) 1 1+4 5 P=300 x( +2 ) x =300 x( x =300 x( x P=300 x x 2 2 ) 2 ) 2 2 2 2 2 To maximize profit, the first derivative must be equal to zero: ' ' ' 5 ' 5 5 5 P' =0 300 x x 2 =0 ( 300 x ) x 2 =0 300 ( x 2 ) =0 300 ( 2 x )=0 2 2 2 2 ( ) 3005 x=0 300=5 x ( ) 300 =x x=60 5 Replacing x in the equation of p: 1 1 x=60 p=400 x=400 ( 60 )=40030 p=370 2 2 Replacing x in the equation of P: 5 5 5 x=60 P=300 x x2 =300 (60 ) ( 60 )2=18,000 ( 3,600 )=18,0009,000 2 2 2 P=9,000 (a) 60 units (b) $ 370 per unit (c) $ 9,000 6. Demand function : p=1210.5 x Cost function :C=50 x +38.75 Revenue : R= px Replacing p in the equation of R: R= px=( 1210.5 x ) x R=121 x0.5 x 2 Profit : P=RC Replacing R and C in the equation of P: P=RC=( 121 x 0.5 x 2 ) ( 50 x +38.75 ) =121 x0.5 x 250 x38.75 2 P=71 x0.5 x 38.75 To maximize the profit P, the first derivative must be equal to zero: ' ' P' =0 ( 71 x0.5 x 238.75 ) =0 ( 71 x )' ( 0.5 x 2 ) ( 38.75 )' =0 ' 710.5 ( x 2 ) 0=0 710.5 ( 2 x )=0 71x=0 x=71 Replacing x in the equation of p: x=71 p=1210.5 x=1210.5 ( 71 )=12135.5 p=85.5 Replacing x in the equation of C: x=71 C=50 x+ 38.75=50 ( 71 )+ 38.75=3,550+38.75 C=3,588.75 C = 3,588.75 C=50.54577464 Average cost : C= C 50.55 x 71 (a) $ 85.5 per unit (b) $ 50.55 per unit 3 2 P=0.1 s + 6 s + 400 7. To maximize the profit P, the first derivative must be equal to zero: ' ' ' P' =0 P' = (0.1 s3 +6 s2 + 400 ) =0 P' =( 0.1 s3 ) + ( 6 s2 ) + ( 400 )' =0 ' 3 ' 2 ' ' 2 ' 2 P =0.1 ( s ) +6 ( s ) +0=0 P =0.1 ( 3 s ) +6 ( 2 s )=0 P =0.3 s +12 s=0 P' =s (0.3 s+12 ) =0 { s 1=0, It is not a solution 12 0.3 s+12=0 12=0.3 s =s s 2=40 0.3 The amount of advertising that maximizes the profit is s=40 To find the point of diminishing returns, the second derivative of the profit must be equal to zero: ' ' ' ' P' ' =0 ( P' ) =0 (0.3 s 2+12 s ) =0 ( 0.3 s 2 ) + (12 s )' =0 0.3 ( s 2 ) +12=0 0.3 ( 2 s ) +12=0 0.6 s +12=0 12=0.6 s 12 =s s=20 0.6 Replacing s in the equation of P: 3 2 3 2 s=20 P=0.1 s + 6 s + 400=0.1 ( 20 ) +6 ( 20 ) +400=0.1 ( 8,000 )+ 6 ( 400 ) + 400 P=800+2,400+ 400 P=2,000 The point of diminishing returns is 8. ( s , P ) =( 20,2,000 ) p1=40 x 1=224 p2= p1 +5=40+5 p2 =45 x 2=204 Assuming that the demand function p is linear: p p1=m ( xx 1 ) Slope : m= p 2 p1 4540 5 = = m=0.25 x 2x 1 204224 20 Replacing m in the demand function p: p p1=m ( xx 1 ) p40=0.25 ( x224 ) p40=0.25 x +56 p=0.25 x+ 56+40 p=0.25 x+ 96 Revenue : R= px Replacing p in the equation of R: R= px=(0.25 x+ 96 ) x R=0.25 x2 + 96 x To get the maximum Revenue R, the first derivative must be equal to zero: ' ' ' R' =0 (0.25 x 2 +96 x ) =0 ( 0.25 x 2 ) + ( 96 x )' =0 0.25 ( x 2 ) + 96=0 0.25 ( 2 x )+ 96=0 0.5 x+ 96=0 96=0.5 x 96 =x x=192 0.5 Replacing x in the equation of p: x=192 p=0.25 x +96=0.25 ( 192 ) +96=48+ 96 p=48 The price per unit will yield a maximum total revenue is $ 48