Fill in missing code below and run in python

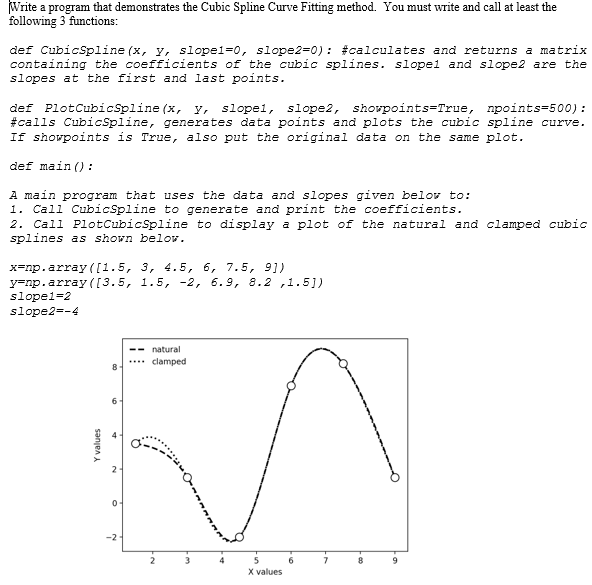
import numpy as np import matplotlib.pyplot as pyplot from scipy import linalg def ClampedCubicSpline(x,y, slope1, slope2): #the goal is to create a set of equations in the form [A][g'']=[b] where [A] is a tri-diagonal matrix, [g''] is a vector of #second derivatives at each x value, and [b] is a vector that is a function of x blen=len(x) A=np.zeros([blen,blen]) b=np.zeros(blen) for i in range(blen): if i==0: dX=x[i+1]-x[i] #deltaX for i A[i][i]=-dX/3 A[i][i+1]=-dX/6 b[i]=slope1+y[i]/dX-y[i+1]/dX elif i==(blen-1): dXl=x[i]-x[i-1] #deltaX for i-1 A[i][i]=-dX/3 A[i][i-1]=-dX/6 b[i]=slope2+y[i-1]/dXl-y[i]/dXl else: dX=x[i+1]-x[i] #deltaX for i dXl=x[i]-x[i-1] #deltaX for i-1 dX2=dX+dXl #deltaX for i + deltaX for i-1 mu=dXl/dX lam=dX2/dX A[i][i-1]=mu A[i][i]=2*lam A[i][i+1]=1 b[i]=6*((y[i+1]-y[i])/dX**2+(y[i-1]-y[i])/(dXl*dX)) ddg=linalg.solve(A,b) return ddg def NaturalCubicSpline(x,y): #the goal is to create a set of equations in the form [A][g'']=[b] where [A] is a tri-diagonal matrix, [g''] is a vector of #second derivatives at each x value, and [b] is a vector that is a function of x blen=len(x) A=np.zeros([blen,blen]) b=np.zeros(blen) for i in range(blen): if i==0 or i==(blen-1): A[i][i]=1 b[i]=0 else: dX=x[i+1]-x[i] #deltaX for i dXl=x[i]-x[i-1] #deltaX for i-1 dX2=dX+dXl #deltaX for i + deltaX for i-1 mu=dXl/dX lam=dX2/dX A[i][i-1]=mu A[i][i]=2*lam A[i][i+1]=1 b[i]=6*((y[i+1]-y[i])/dX**2+(y[i-1]-y[i])/(dXl*dX)) ddg=linalg.solve(A,b) return ddg def interp(x, xvals,yvals,ddg): #given the vector of second derivatives find the value for F(x) nX=len(xvals) xi=0 for i in range(nX): if x 
 
  Write a program that demonstrates the Cubic Spline Curve Fitting method. You must write and call at least the following 3 functions: def CubicSpline (x, y, slopei=o, slope2=0): #calculates and returns a matrix containing the coefficients of the cubic splines. slopel and slope are the slopes at the first and last points. def PlotCubicSpline (x, y, slopei, slope2, showpoints=True, npoints=500): #calls CubicSpline, generates data points and plots the cubic spline curve. If showpoints is True, also put the original data on the same plot. def main(): A main program that uses the data and slopes given below to: 1. Call CubicSpline to generate and print the coefficients. 2. Call PlotCubicSpline to display a plot of the natural and clamped cubic splines as shown below. x=np.array([1.5, 3, 4.5, 6, 7.5, 9]) y=np.array([3.5, 1.5, -2, 6.9, 8.2 ,1.51) slope1=2 slope2=-4 natural clamped 8 6 + Y values 2 0 -2 8 9 X values  Write a program that demonstrates the Cubic Spline Curve Fitting method. You must write and call at least the following 3 functions: def CubicSpline (x, y, slopei=o, slope2=0): #calculates and returns a matrix containing the coefficients of the cubic splines. slopel and slope are the slopes at the first and last points. def PlotCubicSpline (x, y, slopei, slope2, showpoints=True, npoints=500): #calls CubicSpline, generates data points and plots the cubic spline curve. If showpoints is True, also put the original data on the same plot. def main(): A main program that uses the data and slopes given below to: 1. Call CubicSpline to generate and print the coefficients. 2. Call PlotCubicSpline to display a plot of the natural and clamped cubic splines as shown below. x=np.array([1.5, 3, 4.5, 6, 7.5, 9]) y=np.array([3.5, 1.5, -2, 6.9, 8.2 ,1.51) slope1=2 slope2=-4 natural clamped 8 6 + Y values 2 0 -2 8 9 X values