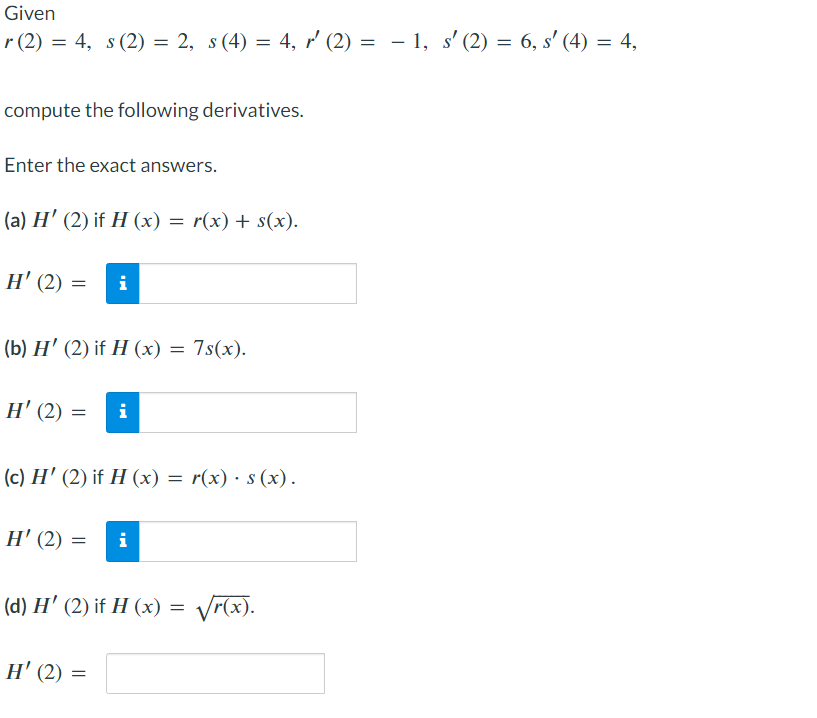
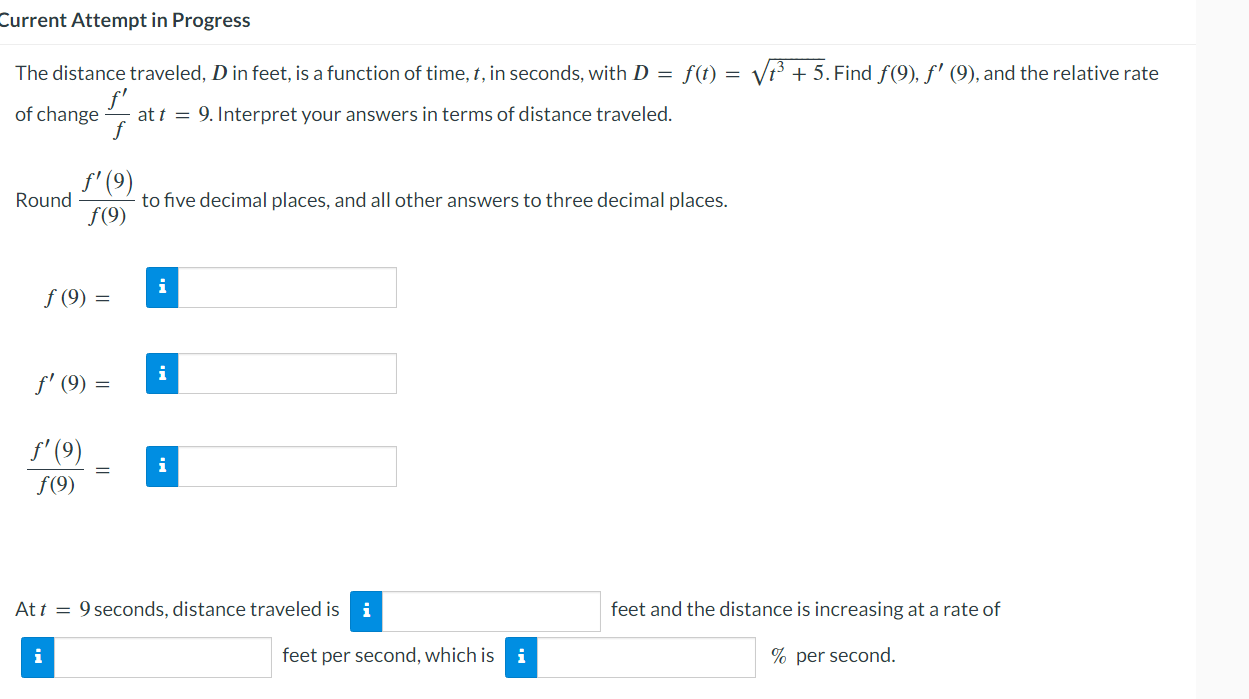
Find the derivative. h'(t) h(t) = ln(et 4t) - Given s' r(2) = 4, s (2) = 2, s (4) = 4, r' (2) = 1, s' (2) = 6, s (4) = 4, compute the following derivatives. Enter the exact answers. (a) H' (2) if H (x) = r(x) + s(x). H' (2) = i (b) H' (2) if H (x) = 7s(x). H' (2) = i (c) H' (2) if H (x) = r(x) s(x). H' (2) = i (d) H' (2) if H (x) = r(x). H' (2) = Current Attempt in Progress The distance traveled, D in feet, is a function of time, t, in seconds, with D = f(t) = + 5. Find (9), ' (9), and the relative rate att = 9. Interpret your answers in terms of distance traveled. of change f Round f'(9) f(9) to five decimal places, and all other answers to three decimal places. i f(9)= i ' (9) = '(9) f(9) i Att = 9 seconds, distance traveled is i i feet per second, which is i feet and the distance is increasing at a rate of % per second.