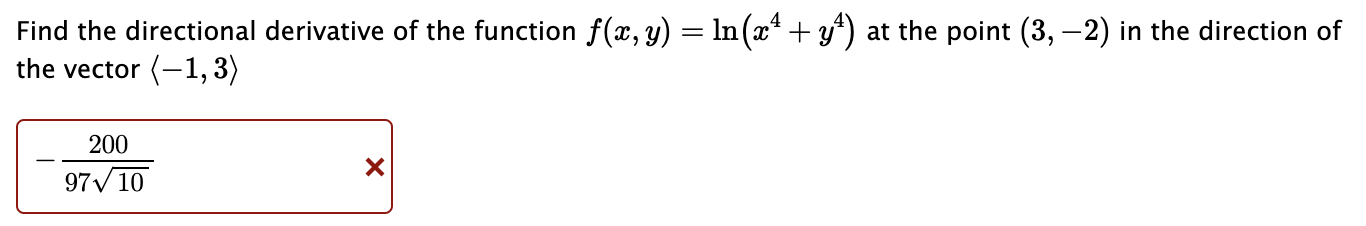
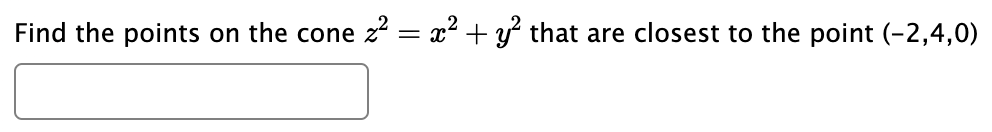
Find the directional derivative of the function f(x, y) = ln(x + y) at the point (3, -2) in the direction of the vector (-1,3) 200 9710 4.x . The gradient of f(x, y) = e sin(1 y) at (x, y) = (-3, 2) is defined as followed: f(x, y) = (fx(3, 2), fy(3, 2)). Then fx(-3,2) = fy(-3,2) = Find the values of x, y and z that correspond to the critical point of the function f(x, y) = 2x - 5x - 2y + 3y: x= 0.4222 y= 0.6224 z= 4.0866 Find the values of x, y and z that correspond to the critical point of the function: z = f(x, y) = 4x - 4x+5y + 3y + 3xy Enter your answer as a decimal number, or a calculation (like 22/7) x= (Round to 4 decimal places) y= (Round to 4 decimal places) z= (Round to 4 decimal places) Find and classify the critical points of z = (x - 8x) (y 2y) Local maximums: Local minimums: Saddle points: - For each classification, enter a list of ordered pairs (x, y) where the max/min/saddle occurs. If there are no points for a classification, enter DNE. Find the absolute maximum and minimum values of f(x, y) = 3x + 5y within the domain x + y 1. 1. Absolute minimum value of f(x, y) is -5.822 2. Absolute maximum value of f(x, y) is 5.822 Find the points on the cone z = x+ y that are closest to the point (-2,4,0)