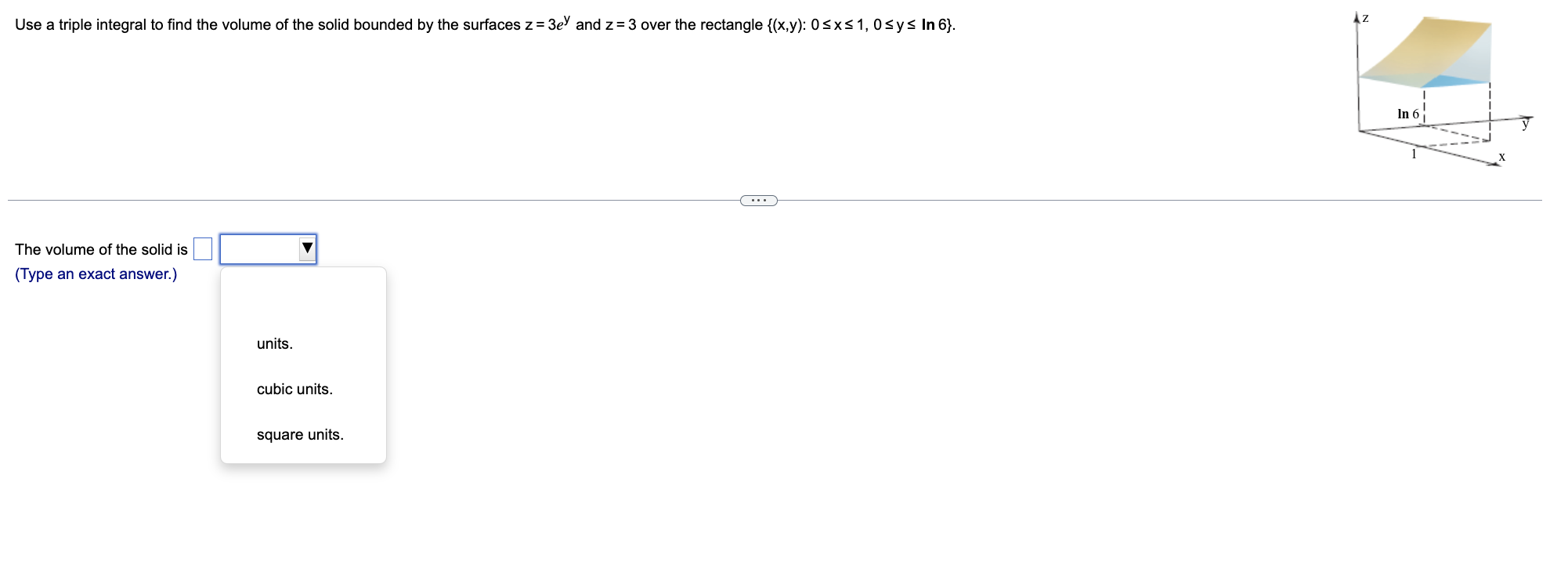
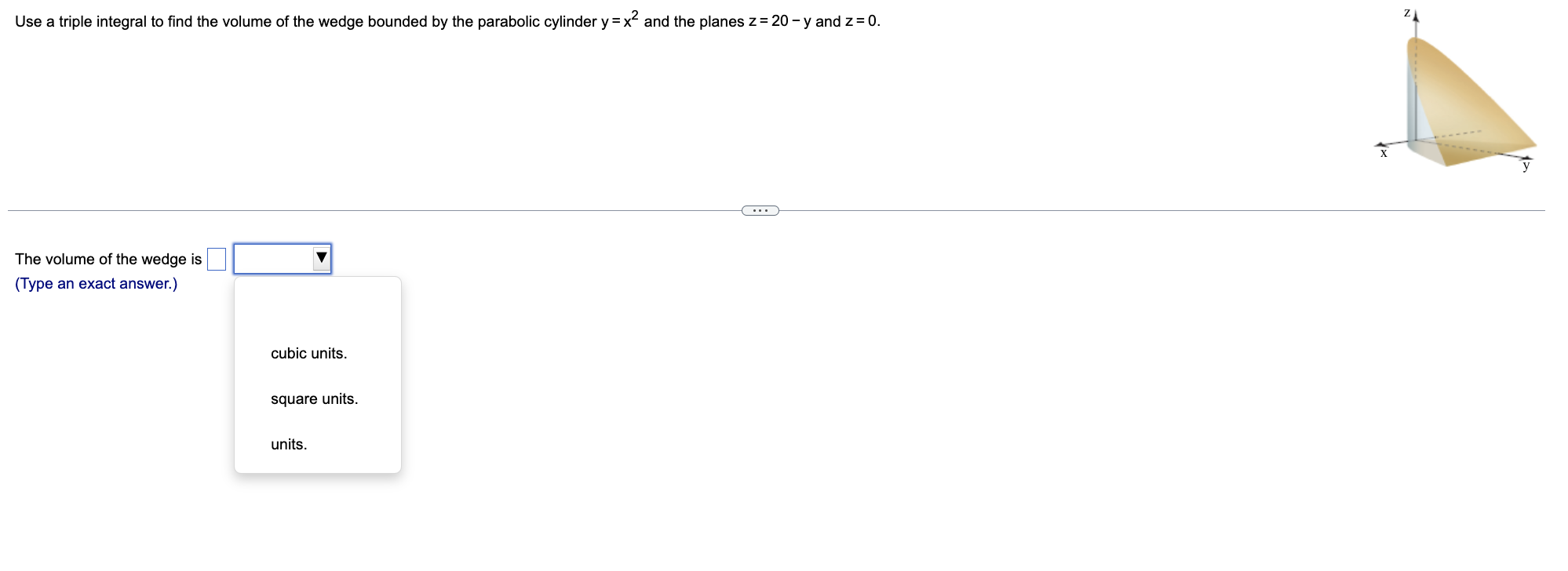
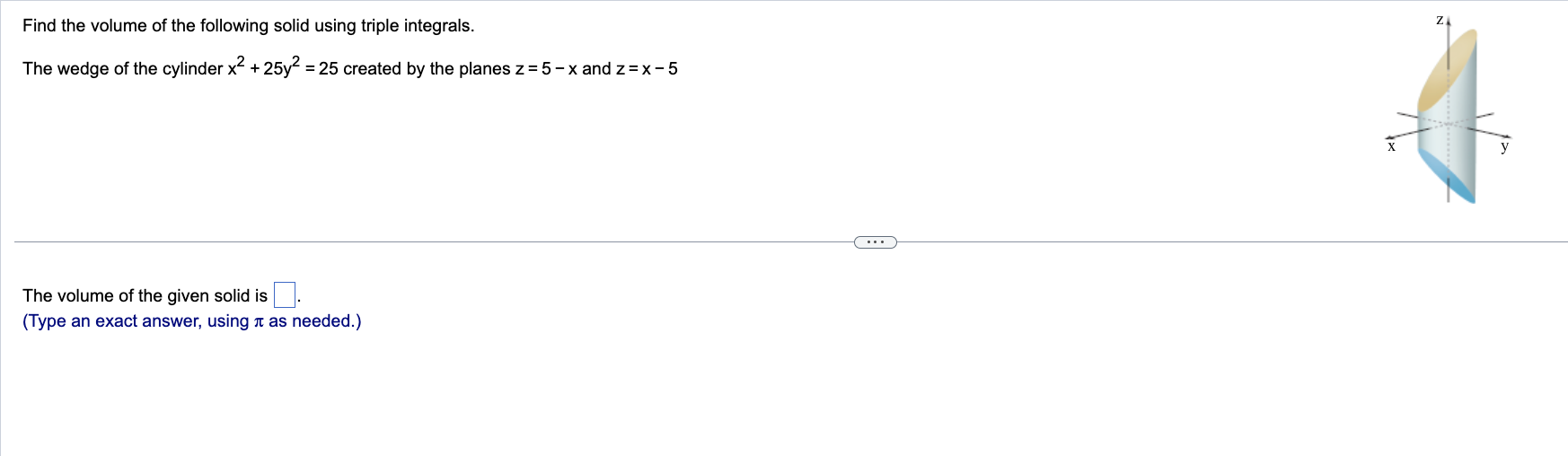
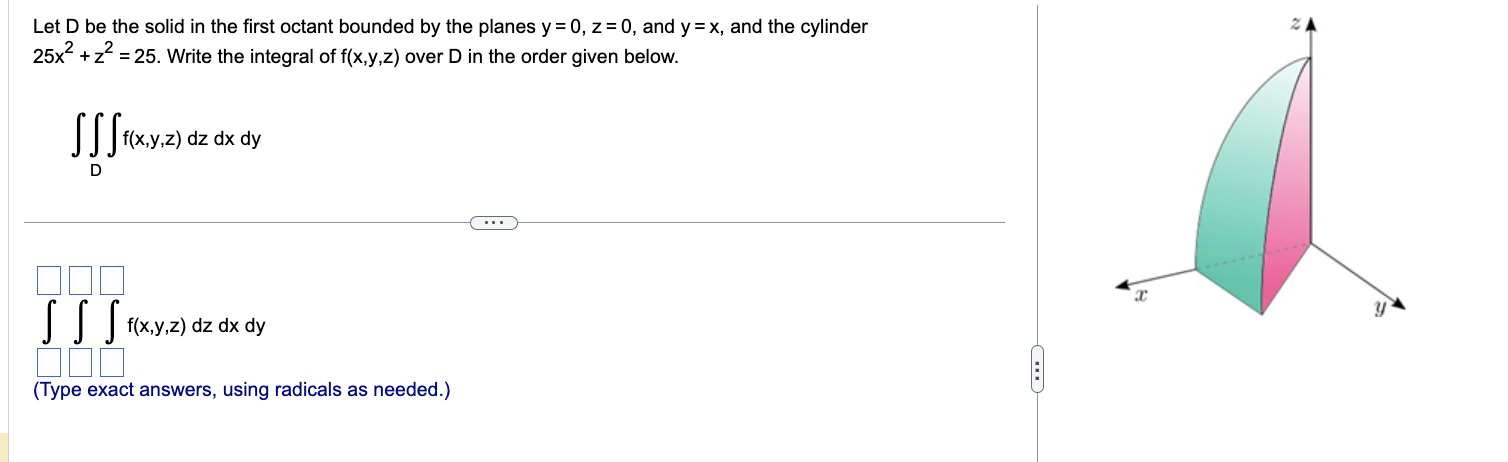
Find the volume of the given solid region in the first octant bounded by the plane 6x+6y+4z 12 and the coordinate planes, using triple integrals. Complete the triple integral below used to find the volume of the given solid region. Note the order of integration dz dy dx. = -111--- 0 0 0 dz dy dx Use a triple integral to find the volume of the solid bounded by the surfaces z=3e and z = 3 over the rectangle {(x,y): 0x 1, 0 y In 6}. The volume of the solid is (Type an exact answer.) units. cubic units. square units. In 6 Use a triple integral to find the volume of the wedge bounded by the parabolic cylinder y = x and the planes z = 20 - y and z = 0. The volume of the wedge is (Type an exact answer.) cubic units. square units. units. 2 Use a triple integral to find the volume of the solid bounded below by the cone z = (x + y and bounded above by the sphere x + y + z = 200. The volume of the solid is (Type an exact answer.) cubic units. square units. units. (0,0,200) x + y+z = 200 Z= Find the volume of the following solid using triple integrals. The wedge of the cylinder x + 25y = 25 created by the planes z = 5-x and z=x-5 The volume of the given solid is (Type an exact answer, using as needed.) X y Let D be the solid in the first octant bounded by the planes y = 0, z = 0, and y=x, and the cylinder 25x2 +z = 25. Write the integral of f(x,y,z) over D in the order given below. +; SSS f(x,y,z) dz dx a D DON SSS f(x,y,z) dz dx dy (Type exact answers, using radicals as needed.) y