Following first 3 images are for are sample which should be followed t solve the answer

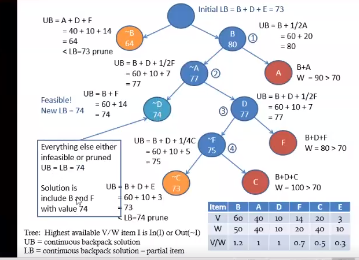
Please give the answer ASAP and briefly explain how to get upper and lower bound as well as most cost-efficient allocation of tasks to workers by branch and bound strategy. Thanks!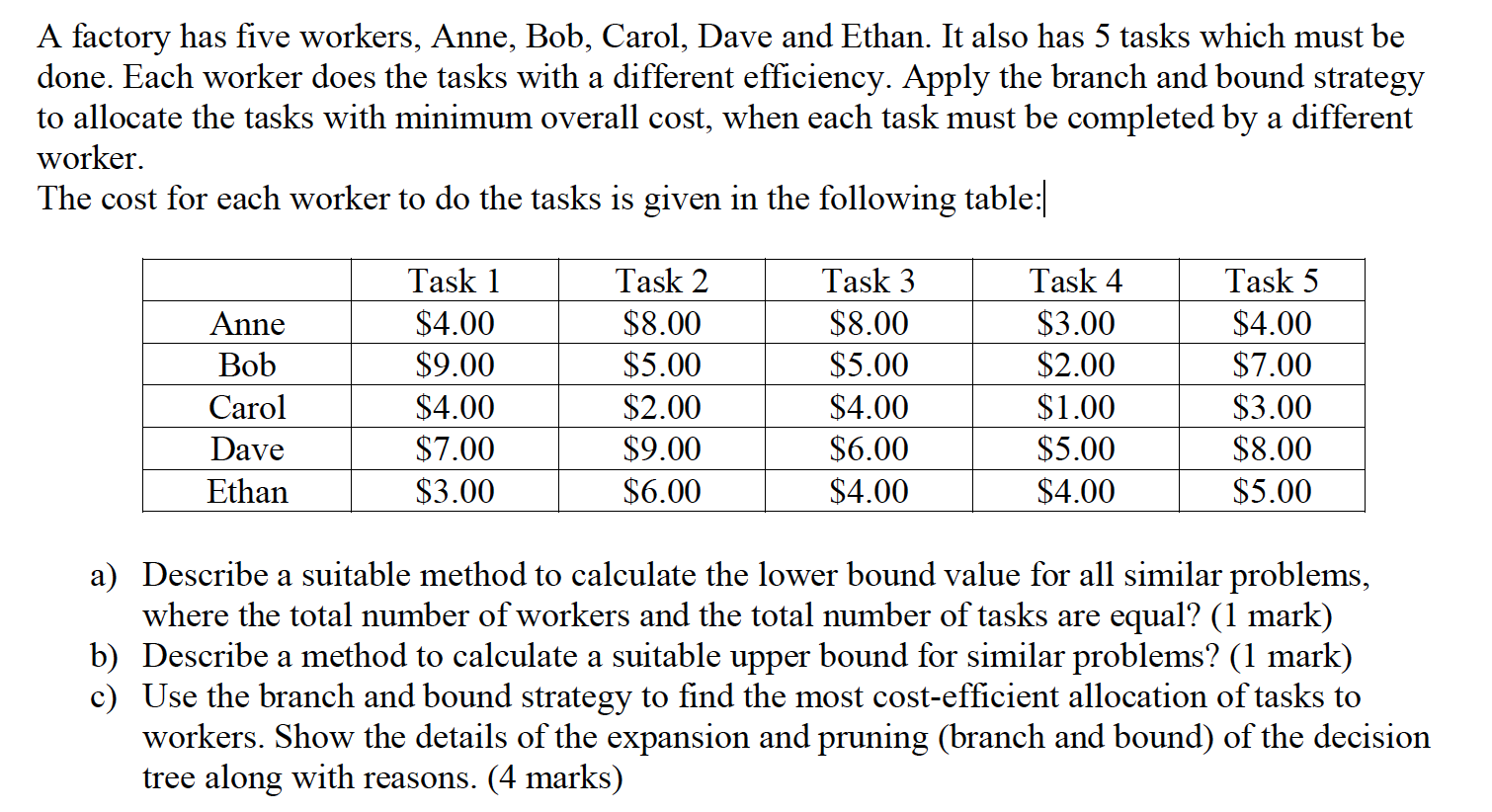

The discrete backpack problem Consider the discrete backpack problem: . We have a set of objects, each with a weight and a value. We need to assemble the greatest possible value into our backpack. . We must put all of an object in the backpack We wish to solve this problem using branch and bound 1. What can we use as an upper bound? 2. What can we use as a lower bound? 3. How can we best construct the state tree? Sample Problem Use the following sample problem to examine your strategy. Item A B D E F Value 60 20 10 3 14 Weight 140 50 40 10 10 20 Backpack capacity = 70 Initial LB=B+D+E=73 UB-B-1/2 B = 60 + 20 80 = 80 UB-A+D+F = 40 + 10 + 14 -B = 64 64 70 infeasible or pruned -75 UB-LB - 74 B+D+C Solution is UB+B+D+E W-100> 70 include Brod 60+ 10+ 3 with value 74 73 Item B ADFC E 18-74 prune V 60 40 1014 3 Tree: Highest available V/WItem Its Intl) or Out-1) w 10 40 10 UB = continuous backpack solution VW 1.2 0.7 0.5 0.3 LB = contimous backpack solution - portal item 20 50 40 1 1 A factory has five workers, Anne, Bob, Carol, Dave and Ethan. It also has 5 tasks which must be done. Each worker does the tasks with a different efficiency. Apply the branch and bound strategy to allocate the tasks with minimum overall cost, when each task must be completed by a different worker. The cost for each worker to do the tasks is given in the following table: Anne Bob Carol Dave Ethan Task 1 $4.00 $9.00 $4.00 $7.00 $3.00 Task 2 $8.00 $5.00 $2.00 $9.00 $6.00 Task 3 $8.00 $5.00 $4.00 $6.00 $4.00 Task 4 $3.00 $2.00 $1.00 $5.00 $4.00 Task 5 $4.00 $7.00 $3.00 $8.00 $5.00 a) Describe a suitable method to calculate the lower bound value for all similar problems, where the total number of workers and the total number of tasks are equal? (1 mark) b) Describe a method to calculate a suitable upper bound for similar problems? (1 mark) c) Use the branch and bound strategy to find the most cost-efficient allocation of tasks to workers. Show the details of the expansion and pruning (branch and bound) of the decision tree along with reasons. (4 marks) The discrete backpack problem Consider the discrete backpack problem: . We have a set of objects, each with a weight and a value. We need to assemble the greatest possible value into our backpack. . We must put all of an object in the backpack We wish to solve this problem using branch and bound 1. What can we use as an upper bound? 2. What can we use as a lower bound? 3. How can we best construct the state tree? Sample Problem Use the following sample problem to examine your strategy. Item A B D E F Value 60 20 10 3 14 Weight 140 50 40 10 10 20 Backpack capacity = 70 Initial LB=B+D+E=73 UB-B-1/2 B = 60 + 20 80 = 80 UB-A+D+F = 40 + 10 + 14 -B = 64 64 70 infeasible or pruned -75 UB-LB - 74 B+D+C Solution is UB+B+D+E W-100> 70 include Brod 60+ 10+ 3 with value 74 73 Item B ADFC E 18-74 prune V 60 40 1014 3 Tree: Highest available V/WItem Its Intl) or Out-1) w 10 40 10 UB = continuous backpack solution VW 1.2 0.7 0.5 0.3 LB = contimous backpack solution - portal item 20 50 40 1 1 A factory has five workers, Anne, Bob, Carol, Dave and Ethan. It also has 5 tasks which must be done. Each worker does the tasks with a different efficiency. Apply the branch and bound strategy to allocate the tasks with minimum overall cost, when each task must be completed by a different worker. The cost for each worker to do the tasks is given in the following table: Anne Bob Carol Dave Ethan Task 1 $4.00 $9.00 $4.00 $7.00 $3.00 Task 2 $8.00 $5.00 $2.00 $9.00 $6.00 Task 3 $8.00 $5.00 $4.00 $6.00 $4.00 Task 4 $3.00 $2.00 $1.00 $5.00 $4.00 Task 5 $4.00 $7.00 $3.00 $8.00 $5.00 a) Describe a suitable method to calculate the lower bound value for all similar problems, where the total number of workers and the total number of tasks are equal? (1 mark) b) Describe a method to calculate a suitable upper bound for similar problems? (1 mark) c) Use the branch and bound strategy to find the most cost-efficient allocation of tasks to workers. Show the details of the expansion and pruning (branch and bound) of the decision tree along with reasons. (4 marks)