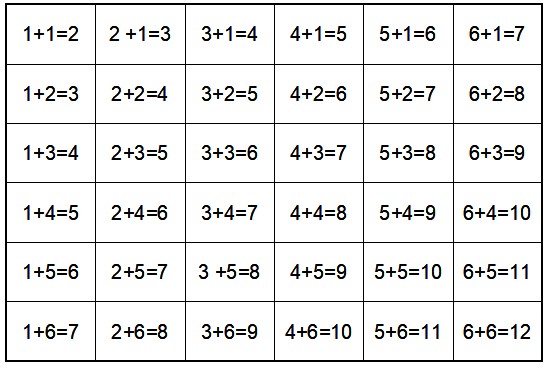
For Questions 1 - 3:For two equally balanced, 6-sided die that are tossed, the following table represents the entire probability space where the first number represents the number on the first die, the second number represents the number on the second die and the third number represents the sum of both numbers (total dots on both die).That is, First Number + Second Number = Total Number.Assume an equally likely (uniform) distribution of simple events.

Let A be the event that at least one of the die was a 3

Let B be the event that doubles (both die are the same) was rolled

Let C be the event that a sum of 5 was rolled

1. Find:

a. N, the total number of possible outcomes from any single event

b.P(A)

c.P(B)

d.P(C)

e.P(A AND B)

f.Are events A and B mutually exclusive?

g.P(A OR B)

h.P(NOT(A AND B))

i. P(NOT(A OR B))

j.P(A | B)

k.P(B | A)

l.Are events A and B independent? Please show formulas used.

2.Find:

a.P(A AND C)

b.Are events A and C mutually exclusive?

c.P(A OR C)

d.P(NOT(A AND C))

e. P(NOT(A OR C))

f.P(A | C)

g.P(C | A)

h.Are events A and C independent? Please show formulas used.

3.Find:

a. P(B AND C)

b.Are events B and C mutually exclusive?

c.P(B OR C)

d.P(NOT(B AND C))

e. P(NOT(B OR C))

f.P(B | C)

g.P(C | B)

h.Are events B and C independent? Please show formulas used.

i.On any particular roll of 2 die, is the number on the second die independent of the number on the first die?Explain your answer.

.According to tables provided by the Statistics Quantify Universally Accepted Theory (SQUAT) organization, there is roughly an 45% (p = 0.45) chance that a person aged 20 will get a tattoo before the age of 70.Suppose that three (N = 3) people aged 20 are independently selected at random.

Use the Binomial Probability for this problem.

a.Assumptions:

Are N trials to be performed?

Are two outcomes, success or failure, possible for each trial?

Are the trials independent?

Does the success probability, p, remain the same from trial to trial?

Are all four assumption met?

Even if you do not think the assumptions are met, please proceed with the following steps using the binomial probability distribution.

b.Step 1Identify a success

c.Step 2 Determine p, the success probability

d.Step 3Determine N, the number of trials

Step 4The binomial probability formula for the number of successes, X is .Plug in p and n and determine the binomial probabilities for this problem

e.Find P(X = 2), the probability that exactly 2 will get a tattoo before the age of 70.

f.Find P(X 1), the probability that, at most, one will get a tattoo before the age of 70

g.Find P(X 2), the probability that, at least two will get a tattoo before the age of 70

h.Find m

i.Specific to this problem, what is the meaning of the population mean?

j.Find s²

k.Find s

l.Specific to this problem, what is the meaning of the population standard deviation?

m.Draw the probability distribution for this problem

n.Is this distribution left skewed, symmetric or right skewed?

5.Based on a recent add from the Symantec, 35% of computers have the Norton antivirus program installed.In a simple random sample of 200 scanned computers, it was found that 56 of them actually had Norton antivirus software programs installed.Use the following steps of the One Proportion z-Hypothesis Test with a 0.05 level of significance, , to test the hypothesis that 35% of computers have Norton antivirus software installed. (Note: x = 56 and n = 200)

a.Determine whether both assumptions are met:

Assumption 1:Simple random sample?

Assumption 2:Both np and nq are 10 or greater

Are both assumptions met?

Even if you do not think the assumptions are met, please proceed with the following steps of the One Proportion z-Hypothesis Test Procedure.

b.Step 1State the null and alternative hypotheses.Is this hypothesis test left tailed, two tailed or right tailed?

H₀:

H_A:

Tail:

c.Step 2Decide on the significance level, .

d.Step 3Find the value of the test statistic.

Use the method of your choosing (the Critical-Value Approach or the P-value Approach) for Parts e and f (Steps 4 and 5, respectively).

e.Step 4Find the appropriate variable (z_cv for the Critical-Value Approach or P for the P-value Approach).

f.Step 5Reject H₀ or do not reject H₀?Why? That is, explain your reasoning.

g.Step 6Interpret the results of the hypothesis.

h.Based on this analysis, do 35% of all computers have Norton antivirus software programs installed?Explain your reasoning.

6.Using the same sample data from Problem #5 (56 out of 200 scanned computers actually had Norton antivirus software programs installed), perform a One-Proportion zInterval Procedure to determine the 95% confidence interval for the population proportion, p, of computers that actually have Norton antivirus software programs installed.(Note: x = 56 and n = 200)

a.Determine whether both assumptions are met:

Assumption 1:Simple random sample?

Assumption 2:Both np and nq are 10 or greater

Are both assumptions met?

Even if you do not think the assumptions are met, please proceed with the following steps for the One Proportion z-Interval Procedure for a population proportion.

b.Step 1For a confidence level of 1 - , find z_/2

c.Step 2Find the confidence interval for the population proportion.

d.Step 3Interpret the confidence interval

e.Based on your confidence interval, does this informal test support the same conclusion as the formal results of the hypothesis test of Problem #5?If so, why and if not, why not?

7.Based on a recent simple random sample of CoC students, 80 of 100 CoC students stated that they would rather attend in person classes than have computer based, synchronized instruction.Use the following steps of the One Proportion z-Hypothesis Test with a 0.05 level of significance, , to test the hypothesis that over 75% of CoC students want to return to having in-person classes. (Note: x = 80 and n = 100)

a.Determine whether both assumptions are met:

Assumption 1:Simple random sample?

Assumption 2:Both np and nq are 10 or greater

Are both assumptions met?

Even if you do not think the assumptions are met, please proceed with the following steps of the One Proportion z-Hypothesis Test Procedure.

b.Step 1State the null and alternative hypotheses.Is this hypothesis test left tailed, two tailed or right tailed?

H₀:

H_A:

Tail:

c.Step 2Decide on the significance level, .

d.Step 3Find the value of the test statistic.

Use the method of your choosing (the Critical-Value Approach or the P-value Approach) for Parts e and f (Steps 4 and 5, respectively).

e.Step 4Find the appropriate variable (z_cv for the Critical-Value Approach or P for the P-value Approach).

f.Step 5Reject H₀ or do not reject H₀?Why? That is, explain your reasoning.

g.Step 6Interpret the results of the hypothesis.

h.Based on this analysis, do over 75% of CoC college students want to return to in-person classes?Explain your reasoning.

8.Using the same sample data from Problem #7 (80 out of 100 CoC students would rather attend in-person classes), perform a One-Proportion zInterval Procedure to determine the 90% confidence interval for the population proportion, p, of all CoC students that would rather attend in-person classes.(Note: x = 80 and n = 100)

a.Determine whether both assumptions are met:

Assumption 1:Simple random sample?

Assumption 2:Both np and nq are 10 or greater

Are both assumptions met?

Even if you do not think the assumptions are met, please proceed with the following steps for the One Proportion z-Interval Procedure for a population proportion.

b.Step 1For a confidence level of 1 - , find z_/2

c.Step 2Find the confidence interval for the population proportion.

d.Step 3Interpret the confidence interval

e.Based on your confidence interval, does this informal test support the same conclusion as the formal results of the hypothesis test of Problem #7?If so, why and if not, why not?

9.Mean Height of Professional Basketball Players. A simple random sample of 40 from a normal population of professional basketball players' heights were measured with a sample mean of 79" and a sample standard deviation was 4".Use the following steps of the One Mean t-Hypothesis Test Procedure with a 0.05 level of significance, , to test the hypothesis that the population mean height of all professional basketball players is greater than 78".(Note: = 79" hours, s = 4" hours and n = 40.)

a.Determine whether all 3 assumptions are met:

Assumption 1:Simple random sample?

Assumption 2:Normal population or large sample size?

Assumption 3: unknown?

Are all 3 assumptions met?

Even if you do not think the assumptions are met, please proceed with the following steps of the One Mean t-Hypothesis Test Procedure.

b.Step 1State the null and alternative hypotheses.Is this hypothesis test left tailed, two tailed or right tailed?

H₀:

H_A:

Tail:

c.Step 2Decide on the significance level, .

d.Step 3 Find the value of the test statistic.

Use the method of your choosing (the Critical-Value Approach or the P-value Approach) for Parts e and f (Steps 4 and 5, respectively).

e.Step 4Find the appropriate variable (t_cv for the Critical-Value Approach or P for the P-value Approach).

f.Step 5Reject H₀ or do not reject H₀?Why?That is, explain your reasoning.

g.Step 6Interpret the results of the hypothesis.

h.Based on this analysis, is the population mean height of all professional basketball payers greater than 78"?Explain your reasoning.

10.Using the same sample data from Problem #9 (40 professional basketball players' heights were measured with a sample mean of 79" and a sample standard deviation was 4"), follow the steps of the One Mean t-Interval Procedure to determine the 90% confidence interval for the population mean height of all professional basketball players.(Note: = 79" hours, s = 4" hours and n = 40.)

a.Determine whether all 3 assumptions are met:

Assumption 1:Simple random sample?

Assumption 2:Normal population or large sample size?

Assumption 3: unknown?

Are all 3 assumptions met?

Even if you do not think the assumptions are met, please proceed with the following steps for the One-Sample t-Interval Procedure for a population mean.

b.Step 1 For a confidence level of 1 - , find t_/2

c.Step 2Find the confidence interval for the population mean.

d.Step 3Interpret the confidence interval

e.Based on your confidence interval, does this informal test support the same conclusion as the formal results of the hypothesis test of Problem #9.If so, why and if not, why not?

11.Extra Credit.Under what two conditions can the population distribution of sample means (for any given sample size) be considered normal?

a.

b.

\f