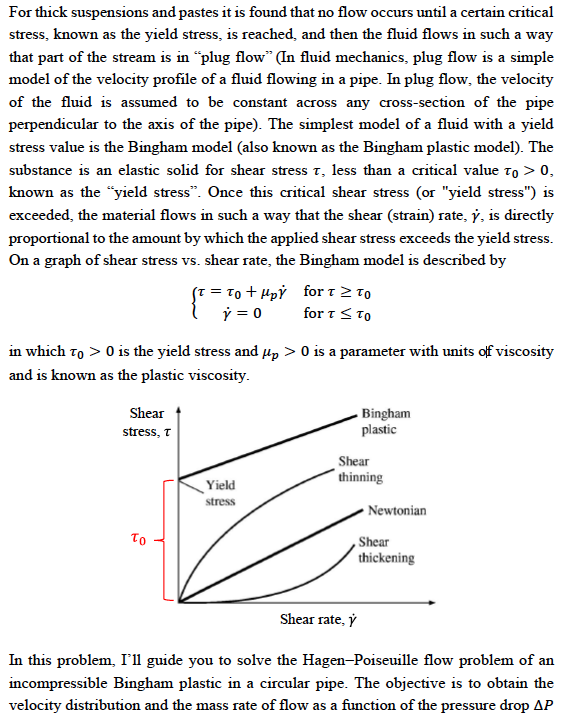
For thick suspensions and pastes it is found that no flow occurs until a certain critical stress, known as the yield stress, is reached, and then the fluid flows in such a way that part of the stream is in plug flow" (In fluid mechanics, plug flow is a simple model of the velocity profile of a fluid flowing in a pipe. In plug flow, the velocity of the fluid is assumed to be constant across any cross-section of the pipe perpendicular to the axis of the pipe). The simplest model of a fluid with a yield stress value is the Bingham model (also known as the Bingham plastic model). The substance is an elastic solid for shear stress T, less than a critical value to > 0, known as the "yield stress. Once this critical shear stress (or "yield stress") is exceeded, the material flows in such a way that the shear (strain) rate, , is directly proportional to the amount by which the applied shear stress exceeds the yield stress. On a graph of shear stress vs. shear rate, the Bingham model is described by fr = To + up for 2 To Y = 0 for ISTO in which to >O is the yield stress and up > 0 is a parameter with units of viscosity and is known as the plastic viscosity. Shear stress, T Bingham plastic Shear thinning Yield stress Newtonian Shear thickening Shear rate, In this problem, I'll guide you to solve the Hagen-Poiseuille flow problem of an incompressible Bingham plastic in a circular pipe. The objective is to obtain the velocity distribution and the mass rate of flow as a function of the pressure drop AP a over a pipe length L, given the pipe radius R and properties of the fluid: yield stress To, plastic viscosity Hp, and density p. For simplicity, we consider that the pipe is placed horizontally, and the fluid is flowing from left to right. No-slip B.C. Fully Developed Flow Notice that the velocity profile is shown for the case of a Newtonian fluid. Trz(r) = 1 * = 4), r = -- L Po L PL For steady flow in a circular pipe, it can be shown that the shear stress is given by (Po - PL 14P 2 L This relation of trz(r) and AP/L does not depend on the type of fluidwhether it is Newtonian or non-Newtonian. Task (a): [4 Points] Find the critical radial position where the local shear stress Trz(r) is just equal to the yield stress. This critical radial position, let it be rc, is sometimes referred to as the yield radius. Now consider the case rc