1. For this assignment, you will design, implement and analyze two algorithms to solve the maximum subarray problem. A solution using the nave brute force approach and one using the divide and conquer approach.
2. The maximum subarray problem is defined as follows from Wikipedia: In computer science, the maximum subarray problem is the task of finding a contiguous subarray with the largest sum, within a given one-dimensional array A[1...n] of numbers. Formally, the task is to find indices and with, such that the sum.

   

   is as large as possible. (Some formulations of the problem also allow the empty subarray to be considered; by convention, the sum of all values of the empty subarray is zero.) Each number in the input array A could be positive, negative, or zero.

   For example, for the array of values [2, 1, 3, 4, 1, 2, 1, 5, 4], the contiguous subarray with the largest sum is [4, 1, 2, 1], with sum 6.

   Some properties of this problem are: a).If the array contains all non-negative numbers, then the problem is trivial; the maximum subarray is the entire array. b). If the array contains all non-positive numbers, then the solution is the number in the array with the smallest absolute value (or the empty subarray, if it is permitted) c). Several different sub-arrays may have the same maximum sum. This problem can be solved using several different algorithmic techniques, including brute force, divide and conquer, dynamic programming, and reduction to shortest paths. 3. Design an algorithm to solve this problem using brute force. The idea is a loop over the all the possible i,j indices i.e. all possible subarrays and computes each sum, keeping track of the subarray with the maximum sum you have found so far and its value. a. Write the pseudocode for your algorithm b. What is the asymptotic running time of your algorithm? Provide an explanation for your answer 4. Design an algorithm to solve this problem using a divide and conquer strategy. To do this consider the following facts. If you split the array in two the maximum subarray could be either in The first half of the array The second half of the array Or straddles the end of the first half and the beginning of the second half, crossing the mid-point of the array 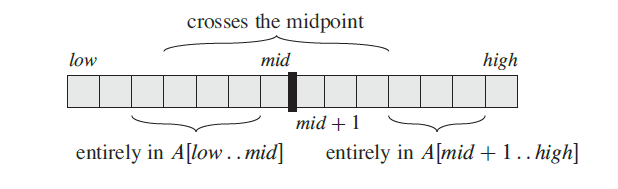The first two cases can then be solved recursively while the third can be solved in linear time. a. Write the pseudocode for your algorithm b. What is the asymptotic running time of your algorithm. Provide an explanation for your answer 5. Using any programming language of your choice implement the algorithms you designed in 3 and 4. above. Use the attached test file to show that your algorithms and implementations are correct. The file has one test case per line (10 cases each with 100 entries). A line corresponding to the example above would be: [31, -41, 59, 26, -53, 58, 97, -93, -23, 84], 187 with the input array followed by the sum of the maximum subarray. Include screenshots in your submission. 6. Experimental Analysis: For the experimental analysis you will plot running times as a function of input size. Every programming language should provide access to a clock. Run each of your algorithms on input arrays of size 100 1000 in increments of 100 (that is, you should have 10 data points for each algorithm). To do this, generate random instances using a random number generator as provided by your programming language. Remember to include both positive and negative numbers! For each data point, you should take the average of a small number (say, 10) runs to smooth out any noise. For example, for the first data point, you will do something like: for i = 1:10 A = random array with 100 entries start clock maxsubarray(A) pause clock return elapsed time Note that you should not include the time to generate the instance. Plot the running times as a function of input size for each algorithm in a single plot. Provide screenshots of your algorithm generating the results. Include the code that runs the experiments in your submission 7. Discuss your plot in 6. Do the theoretical and experimental running times agree? 8. Provide a real-world example of a problem that can be modelled and solved as a maximum subarray problem. 9. Submit a report along with all your implemented code, which should include a detailed readme file (which should explain how to run the code) in separate files via Blackboard by the due date.

crosses the midpoint low weid high nu mid +1 entirely in Allow.. mid] entirely in Almid 1..high entirely in A[mid + 1..high