Question
From various textbooks, I have read that: (1) When a sequence s n as n one writes that the x lim s n = if
From various textbooks, I have read that:
(1) When a sequence sn as n one writes that the xlimsn= if for M>0 , N such that if n > N then sn > M.
(2) When a sequence sn as n one writes that the nlimsn= if for M0 , N such that if n > N then sn I think I can use these two definitions to help me prove the following theorem given that the proof requires me to consider a case where the limit mirrors (1) and the other case mirrors (2). However, these definitions might be unnecessary. what are the proofs for the two cases in the following theorem.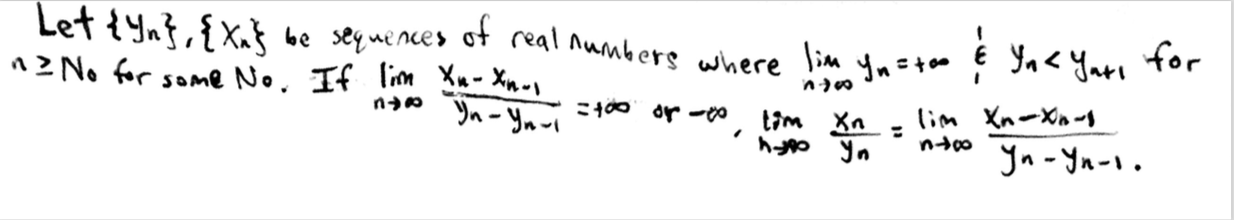
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


