function ex_with_2eqs t0 = 0; tf = 20; y0 = [10;60]; a = .8; b = .01; c = .6; d = .1; [t,y] = ode45(@f,[t0,tf],y0,[],a,b,c,d); u1 = y(:,1); u2 = y(:,2); % y in output has 2 columns corresponding to u1 and u2 figure(1); subplot(2,1,1); plot(t,u1,'b-+'); ylabel('u1'); subplot(2,1,2); plot(t,u2,'ro-'); ylabel('u2'); figure(2) plot(u1,u2); axis square; xlabel('u_1'); ylabel('u_2'); % plot the phase plot end %---------------------------------------------------------------------- function dydt = f(t,y,a,b,c,d) u1 = y(1); u2 = y(2); dydt = [ a*u1-b*u1*u2 ; -c*u2+d*u1*u2 ]; end 

function LAB04ex1 % NOTE: you CAN run this type of function m file as a script because it requires no inputs. Click the Green arrow above the "Run" tab t0 = 0; tf = 40; % initial and final time y0 = [-1; 0];%[y0, v0] [t,Y] = ode45(@f,[t0,tf],y0);% f=system of diff eqs; [t0,tf]

y = Y(:,1); % the output Y has 2 columns corresponding to y and v v = Y(:,2); % the output Y has 2 columns corresponding to y and v

figure(1); plot(t,y,'b-+'); % plots y(t) hold on plot(t,v,'ro-'); % plots v(t) legend('y (t)','v (t)') grid on; figure(2) plot(y,v); % plot solution in the space of y and v (instead of plotting y and v over time) axis square; % makes the figure window square xlabel('y'); ylabel('v'); ylim([-1.5,1.5]); xlim([-1,1]); grid on end %----------------------------------- function dydt = f(t,Y) y = Y(1); v = Y(2);% for EX4 you will need a third element w=Y(3) dYdt = [v; cos(t)-4*v-3*y];%=[dy/dt; dv/dt], the two derivatives as a function of y and v end

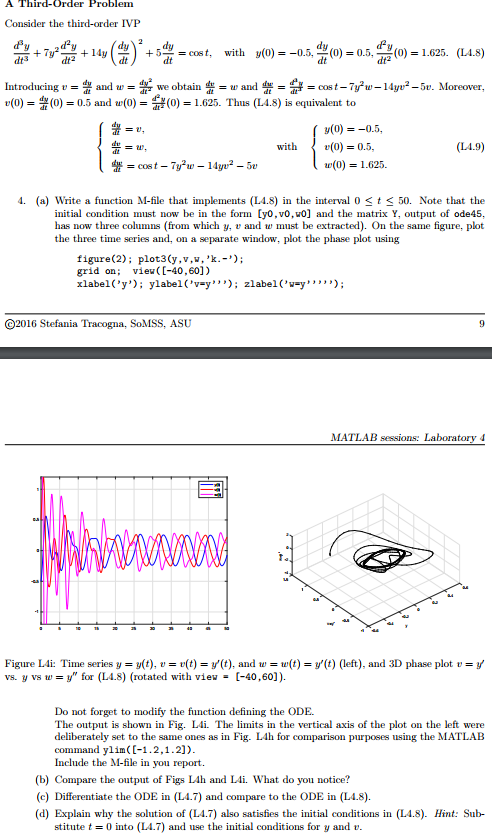
function ex_with_param t0=0; tf=3; y0=1; a=1; [t,y]=ode45(@f,[t0,tf],y0,[],a); disp(['y(',num2str(t(end)),') = ',num2str(y(end))]) disp(['length of y =', num2str(length(y))]) %------------------------------------------------- function dydt=f(t,y,a) dydt=-a*(y-exp(-t))-exp(-t); 

A Third-Order Problem Consider the third-order IVP +5dy=cost, with y(0)=-0.5, dt(0)=0.5, t (0-1.625. (L4.8) w and= = cost-Ty2w-14yt,2-5v. Moreover dt3 dt Introducing u = and w-r we obtain r(0) (0) = 0.5 and w(0- (0) = 1.625. Thus (L4.8) is equivalent to y(0) =-0.5, r(0) = 0.5. u'(0) with (L4.9) 1.625. 4. (a) Write a function M-file that implements (L4.8) in the interval 0