Geometric Proofs

Logical, deductive reasoning requires a systematic way of thinking that outlines steps of mathematical statements to take given information and prove a mathematical statement. This form of reasoning is the backbone for geometric proofs, utilizing definitions, postulates, theorems, and other properties of geometric figures to show that a statement is true. Many geometric proofs involve congruency statements, to be proven using isometric transformations or congruency theorems.

Translation Reflection Rotation

As you complete the task, keep these questions in mind:

How can rigid transformations be used to prove congruency? How can congruency theorems be used to prove congruency?

In this task, you will apply what you have learned in this unit to answer these questions.

Directions

Complete each of the following tasks, reading the directions carefully as you go. Be sure to show all work where indicated, including inserting images of graphs. Be sure that all graphs or screenshots include appropriate information such as titles, labeled diagrams, etc. If your word processing program has an equation editor, you can insert your equations here. Otherwise, print this activity sheet and write your answers by hand.

In addition to the answers you determine, you will be graded based on the work you show, or your solution process. So, be sure to show all your work and answer each question as you complete the tasks. Type all your work into this document, or print the document and show work by hand, so you can submit it to your teacher for a grade. You will be given partial credit based on the work you show and the completeness and accuracy of your explanations.

Your teacher will give you further directions about how to submit your work. You may be asked to upload the document, e-mail it to your teacher, or print it and hand in a hard copy.

Now, let's get started!

Part 1: Use transformations to prove congruency.

1. Given:;

Prove:CBFEDF using isometric (rigid) transformations.

Outline the necessary transformations to proveCBFEDF using a paragraph proof. Be sure to name specific sides or angles used in the transformation and any congruency statements.

Part 2: Use congruency theorems to prove congruency.

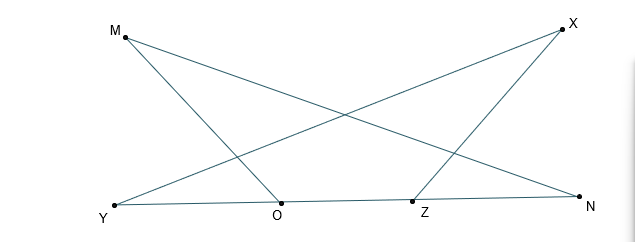
1. The congruency ofrMNO andrXYZ can be proven using a reflection across the line bisecting. However, this congruency can also be proven using geometric postulates, theorems, and definitions. Prove that the triangles are congruent using a two-column proof and triangle congruency theorems.

Given:MX NY

Prove:rMNOrXYZ

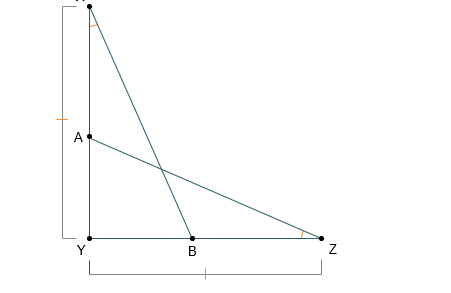
1. Use the diagram and given information to answer the questions and prove the statement.

Given: XZ

Prove:

1. Re-draw the diagram of the overlapping triangles so that the two triangles are separated.

1. What additional information would be necessary to prove that the two triangles,rXBY andrZAY, are congruent? What congruency theorem would be applied?

1. Proveusing a flow chart proof.

Part 3: Choose a proof method.

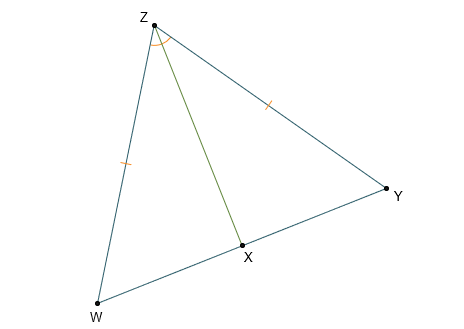
1. Use a paragraph, flow chart, or two-column proof to prove thatis the perpendicular bisector of side.

Given: WZXYZX;

Prove: is a perpendicular bisector of

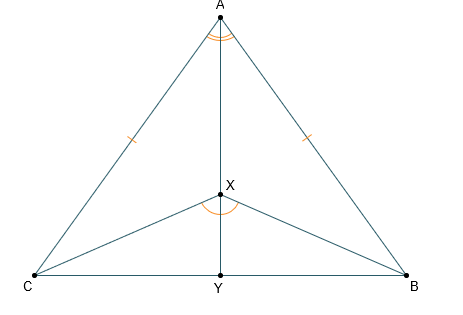
1. Use a paragraph, flow chart, or two-column proof to prove the angle congruency.

Given: CXYBXY CAXBAX

Prove:XCYXBY

M X O NA Z BY X WA X C Y B