Get the solution for the attached problem in matlab code.

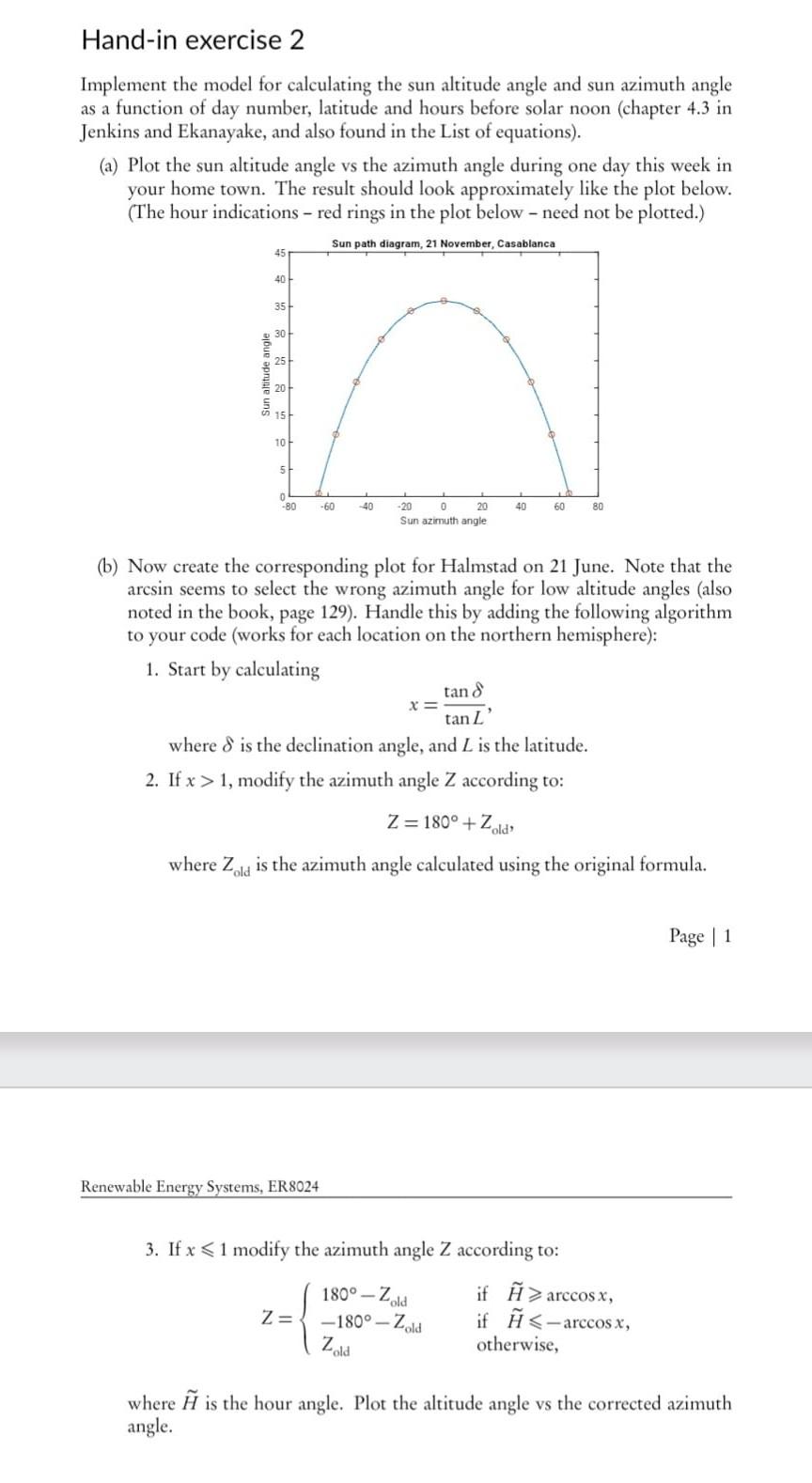
Hand-in exercise 2 Implement the model for calculating the sun altitude angle and sun azimuth angle as a function of day number, latitude and hours before solar noon (chapter 4.3 in Jenkins and Ekanayake, and also found in the List of equations). (a) Plot the sun altitude angle vs the azimuth angle during one day this week in your home town. The result should look approximately like the plot below. (The hour indications - red rings in the plot below - need not be plotted.) Sun path diagram, 21 November, Casablanca Sun altitude 451 40 35 30 25 20 15 10 5 0 -80 -60 -40 -20 0 20 60 80 Sun azimuth angle (b) Now create the corresponding plot for Halmstad on 21 June. Note that the arcsin seems to select the wrong azimuth angle for low altitude angles (also noted in the book, page 129). Handle this by adding the following algorithm to your code (works for each location on the northern hemisphere): 1. Start by calculating x= tan & tan Z where & is the declination angle, and L is the latitude. 2. If x>1, modify the azimuth angle Z according to: Z = 180 + Zold where Z is the azimuth angle calculated using the original formula. Renewable Energy Systems, ER8024 3. If x 1 modify the azimuth angle Z according to: if Harccos x, Z= 180-Zold -180-Zold if