Given a family of intervals [a_i, b_i],i= 1, ..., n, a sub-cover is subset of the intervals that covers the same area of the real line as the union of all the intervals. For example, in the following

picture, the gray intervals form a sub-cover consisting of 5 intervals:

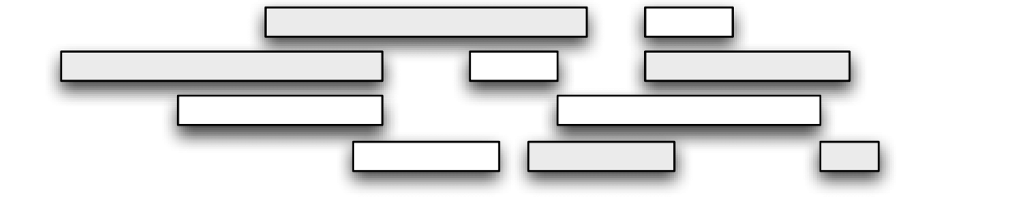
(Warm-up exercise, not to hand in: what is the smallest subcover for this family?) You want to design an efficient algorithm that finds a sub-cover with as few intervals as possible. In the following, you may assume that (i) all the endpoints (a_i, b_i) are distinct, and (ii) the original set of intervals covers a contiguous segment of the real line.

(a)

Your friend suggests the following greedy approach: at each stage, add the interval with

the most length not covered by the intervals selected so far. Give an example showing

that this approach will not find the smallest sub-cover.

(b)

Give a polynomial-time algorithm to find a smallest sub-cover, given the a_is and b_is asinput.

(c)

What is the running time of youralgorithm? Justify.

(d)

Prove that the greedy algorithm is correct.