hash function will now use an instance variable called level. key is as it was before - the key being inserted into the table. level specifies what level of the hash table hierarchy we are hashing for. This will become more obvious with a worked example. You can assume that all keys that go into this table are strings of lowercase english letters.

Using the following hash function:

class InfiniteHashTable
TABLE_SIZE = 27

def hash(self, key: K) -> int:
if self.level < len(key):
return ord(key[self.level]) % (self.TABLE_SIZE-1)
return self.TABLE_SIZE-1

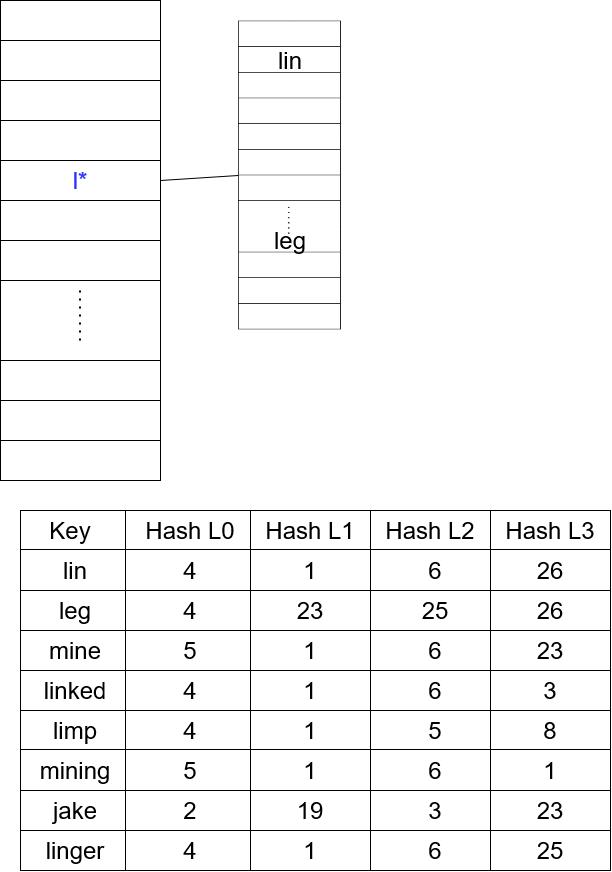
Adding lin and leg, we'd make a new table at the position 4, resulting in the following diagram:

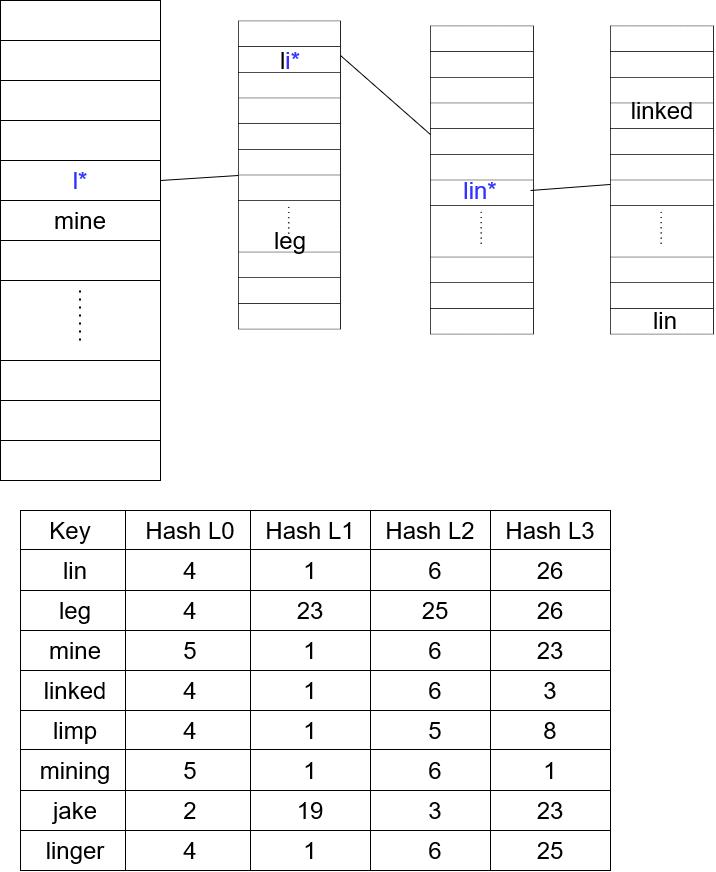
Next, after inserting mine and linked, mine would be inserted at the top level, and what was previously the location for lin now needs to be separated into a new table:

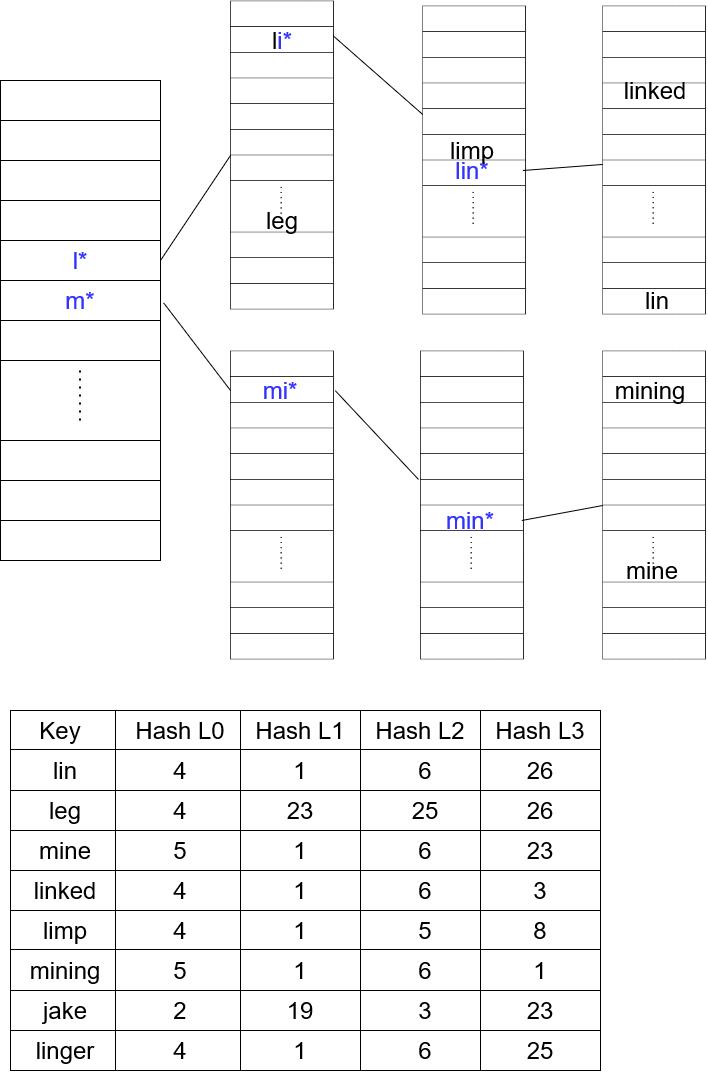
Next, adding limp and mining will first add limp in the table corresponding to li, while mining will split the location formerly hosting mine:

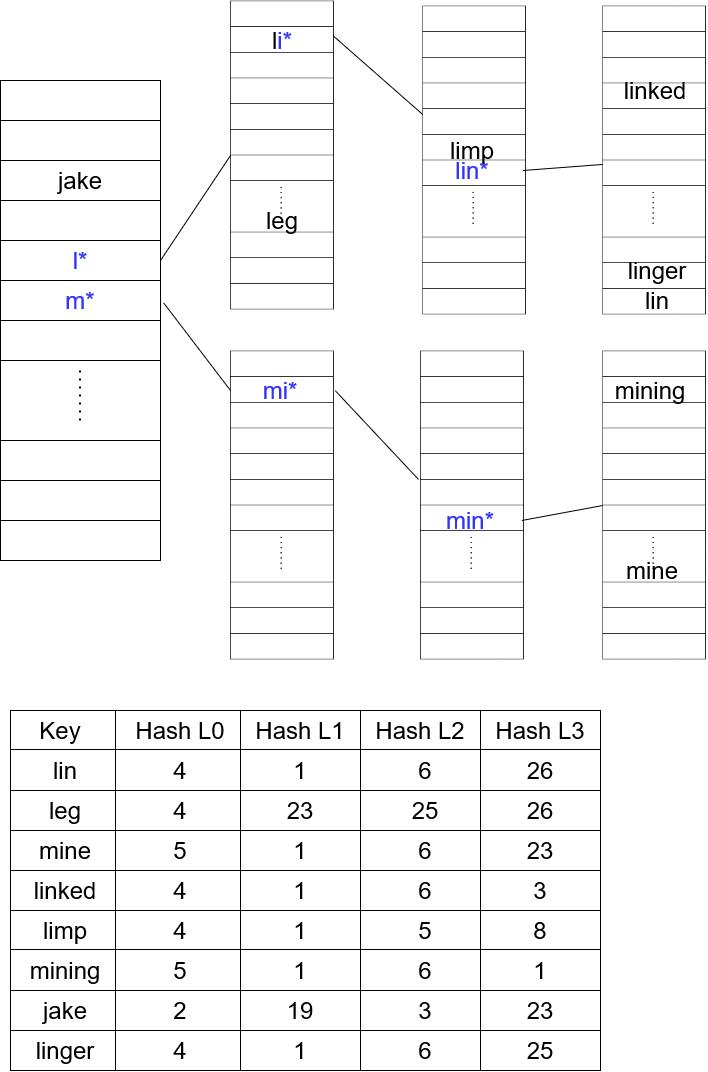
Finally, adding jake just sits at the top level (no collision), and adding linger navigates to the lin* table and inserts there:

sorted function and dict inbuilt type should not be used

task is to define the following methods for InfiniteHashTable:

__init__: Initialises the table. You may add optional arguments here if you like.

__getitem__ : Retrieves a value based on it's key.

__setitem__ : Sets a value based on the key.

__delitem__ : Remove a key/value pair. If this pair removed leaves only a single pair within the current table, then the current table should be collapsed to a single entry in the parent table (This should continue upwards until there is a table with multiple pairs or we are at the top table). See test_delete for an example.

get_location : Returns a list containing the indices required to retrieve a key. In the example above, get_location(linger) == [4, 1, 6, 25]

And finally, after you've implemented everything from before, there's one more function to implement: sort_keys. This function should return all keys that are currently in the table in lexicographically sorted order. Lexicographically sorted simply means that we compare a string letter by letter, and compare using the rule

a<b<c<d<⋯

And prefixes of text are always smaller than the full text. This problem can be solved in O(N∗A∗L), where N is the number of words inserted, L is the length of the longest word and A is the size of the alphabet (26 in our case). Another way of stating this is O(C) where C is the amount of memory taken up by the infinite hash table in bytes (Q: Why are these the same?).

Python:

from _future_ import annotations
from typing import Generic, TypeVar

from data_structures.referential_array import ArrayR

K = TypeVar("K")
V = TypeVar("V")

class InfiniteHashTable(Generic[K, V]):
"""
Infinite Hash Table.

Type Arguments:
- K: Key Type. In most cases should be string.
Otherwise `hash` should be overwritten.
- V: Value Type.

Unless stated otherwise, all methods have O(1) complexity.
"""

TABLE_SIZE = 27

def _init_(self) -> None:
raise NotImplementedError()

def hash(self, key: K) -> int:
if self.level < len(key):
return ord(key[self.level]) % (self.TABLE_SIZE-1)
return self.TABLE_SIZE-1

def _getitem_(self, key: K) -> V:
"""
Get the value at a certain key

:raises KeyError: when the key doesn't exist.
"""
raise NotImplementedError()

def _setitem_(self, key: K, value: V) -> None:
"""
Set an (key, value) pair in our hash table.
"""
raise NotImplementedError()

def _delitem_(self, key: K) -> None:
"""
Deletes a (key, value) pair in our hash table.

:raises KeyError: when the key doesn't exist.
"""
raise NotImplementedError()

def _len_(self) -> int:
raise NotImplementedError()

def _str_(self) -> str:
"""
String representation.

Not required but may be a good testing tool.
"""
raise NotImplementedError()

def get_location(self, key) -> list[int]:
"""
Get the sequence of positions required to access this key.

:raises KeyError: when the key doesn't exist.
"""
raise NotImplementedError()

def _contains_(self, key: K) -> bool:
"""
Checks to see if the given key is in the Hash Table

:complexity: See linear probe.
"""
try:
_ = self[key]
except KeyError:
return False
else:
return True

def sort_keys(self, current=None) -> list[str]:
"""
Returns all keys currently in the table in lexicographically sorted order.
"""
raise NotImplementedError()
 
 
 

* lin ..... leg Key Hash LO Hash L1 Hash L2 Hash L3 lin 4 1 6 26 leg 4 23 25 26 mine 5 1 6 23 linked 4 1 6 3 limp 4 1 5 8 mining 5 1 6 1 jake 2 19 3 23 linger 4 1 6 25