Hello everyone, thanks for the help! I don't understand this problem, somoane can write it in Scratch for me? Please;

This is what I got;

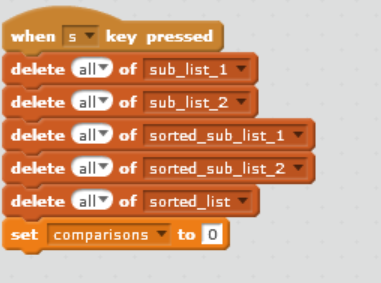
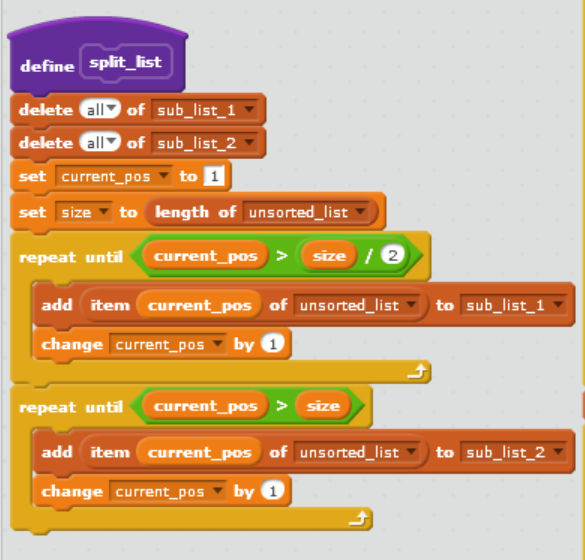
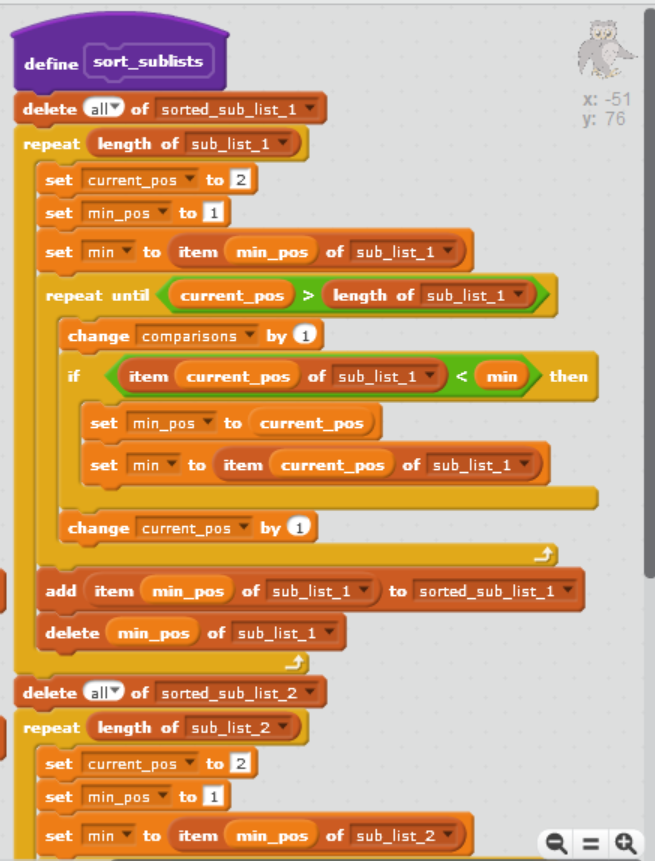
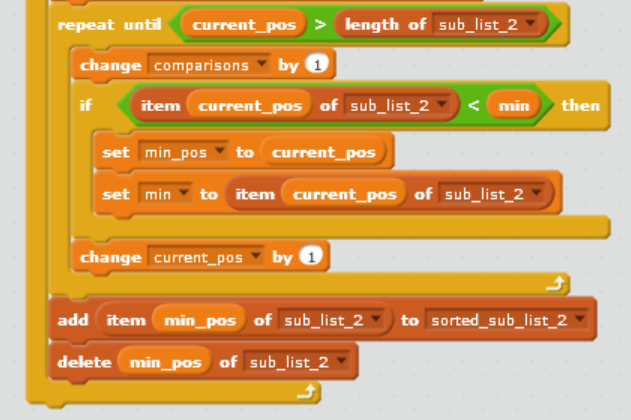
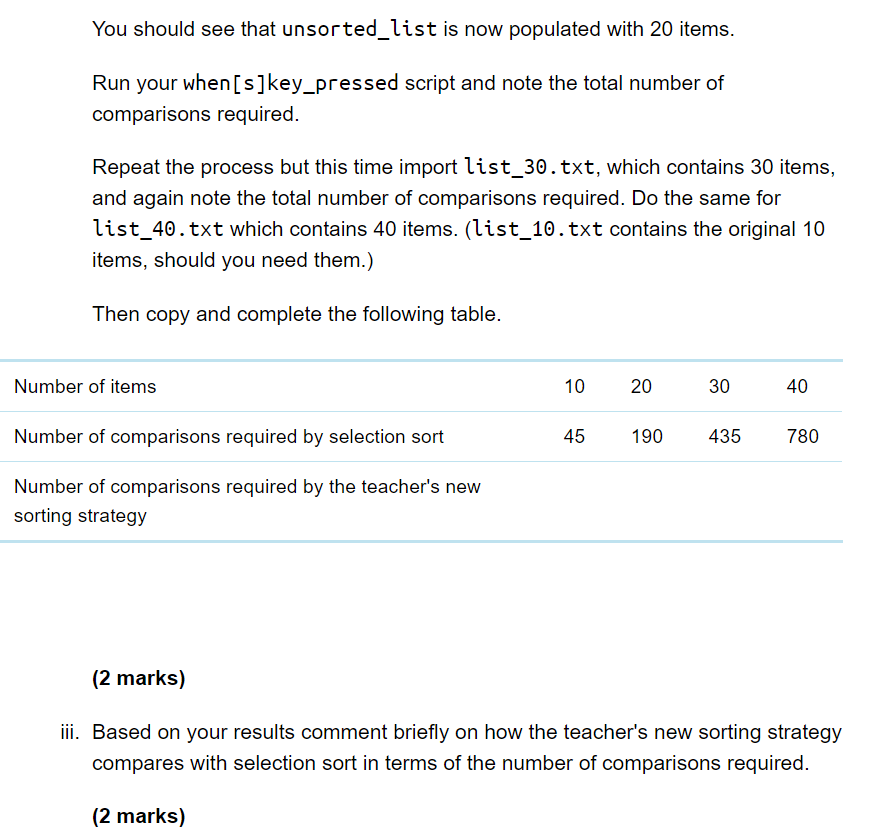
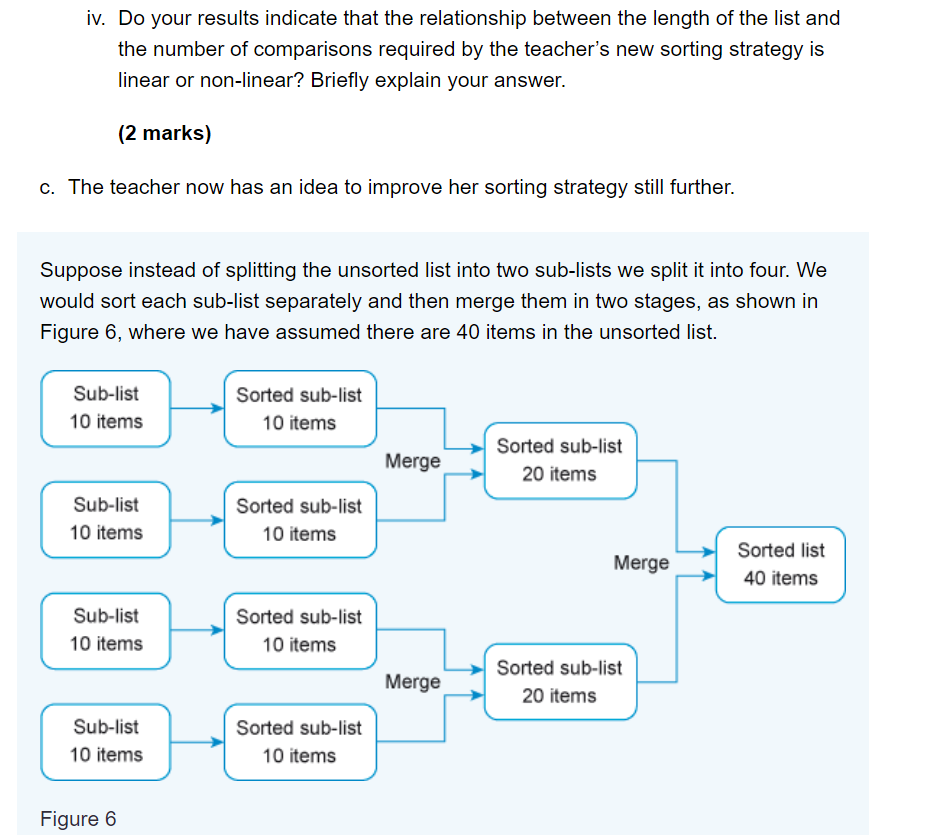
The teacher runs an after-school computing club. Recently she has come up with a new way of sorting, which she thinks will take fewer comparisons than selection sort. She explains her new sorting strategy to you like this: Suppose we want to sort a list of 10 items in random order, for example 3 48 35 72 32 26 52 61 87 15 As you learned in Part 6, using selection sort would require about (10 - 1)212 comparisons. In fact the exact number of comparisons required by selection sort to sort a list of length n is given by the formula nx (n 1)/2, which with n = 10 works out to 45. But suppose we first split the list about its mid-point into two sub-lists of 5 items as follows 3 48 35 72 32 26 52 61 87 15 and sort them each separately? Using the same formula n x (n 1)/2 with n = 5 tells us that sorting each sub-list using selection sort would require 5 x (5 1)/2 = 10 comparisons, so for two sub-lists that would be 2 x 10 = 20 comparisons altogether. When they have been sorted the two sub-lists will be as follows 3 32 35 48 72 15 26 52 61 87 By merging these two sub-lists using an appropriate algorithm we can then produce a new list that represents the desired sort of the original list. Perhaps this will be more efficient! The teacher has begun creating a program in OUBuild to demonstrate her strategy, and she wants you to help her to complete it, and then to investigate how many comparisons her new strategy requires altogether. Open the project TM111_02_Q4.sb2. It contains several lists: unsorted_list which currently contains the 10 items in the example above sub_list_1 and sub_list_2, both currently empty. These will be used to hold the first and second halves of the original list, after it has been split in two sorted_sub_list_1 and sorted_sub_list_2, also both currently empty. These will be used to hold the results of sorting sub_list_1 and sub_list_2 sorted_list which will eventually hold a sorted version of the original unsorted_list. The project also contains a number of variables. The only one of these that you will need to use in your code is comparisons, whose purpose will be explained later. It also contains a when[s]key_pressed script, which at present just empties all the lists except for unsorted_list, and sets the value of comparisons to O. As you work through parts (a) and (b) below you will add to this script. We have also provided two components: a custom block split_list whose purpose is to split the original list into two sub- lists of as near as possible equal length. If the length of the original list is even the sub-lists should be of exactly equal length. If the length of the original list is odd, the length of the second sub-list should be one more than the length of the first sub-list. For example, if we start with a list of 10 items we should get two sub-lists of length 5. If we start with a list of 11 items we should get a first sub-list of length 5 and a second sub-list of length 6. a custom block sort_sublists, which sorts both the sub-lists using a selection sort. You will not be expected to understand this code but you may be interested to look at it. There is no need to change either of these custom block definitions and you should not do so. a. Drag a split_list custom block from the More Blocks palette to the scripts area and add it as the last block in the when[s]key_pressed script, as shown in Figure 3. when s key pressed delete all of sub_list_1 delete all of sub_list_2 delete all of sorted_sub_list_1 delete all of sorted_sub_list_2 delete all of sorted_list set comparisons to O split_list Figure 3 Run the when[s]key_pressed script. You should observe that the unsorted list has been split into two sub-lists. Then drag a sort_sublists custom block from the More Blocks palette to the scripts area and add it below the split_list block. The when[s]key_pressed script should now be as shown in Figure 4. when s key pressed delete all of sub_list_1 delete all of sub_list_2 delete all of sorted_sub_list_1 delete all of sorted_sub_list_2 delete all of sorted_list set comparisons to O split_list sort_sublists Figure 4 Run the when[s]key_pressed script. Both the sub-lists should now be sorted. Recall the teacher's description of her new sorting strategy. There were three stages to it: o spilt the unsorted list into two sub-lists o sort the sub-lists o merge the sorted sub-lists into a single sorted list. The custom blocks you have just added carry out the first two stages. Now you will create a custom block to carry out the final stage. A merge_lists custom block is now required which will merge the two sorted sub- lists into a single sorted list. Consider the algorithm below for achieving this task, and the explanation that follows. Repeat until (length of first sorted sub-list is o or length of second sorted sub-list is o) If item 1 of first sorted sub-list is lower than item l of second sorted sub-list Add item 1 of first sorted sub-list to end of sorted_list Remove this item from first sorted sub-list else Add item I of second sorted sub-list to end of sorted list Remove this item from second sorted sub-list Repeat until (length of first sorted sub-list is O) Add item 1 of first sorted sub-list to end of sorted_list Remove this item from first sorted sub-list Repeat until (length of second sorted sub-list is 0) Add item l of second sorted sub-list to end of sorted_list Remove this item from second sorted sub-list The algorithm works by repeatedly comparing the first items of each sorted sub-list and moving the lowest of the two items to the merged sorted list, until one of the lists becomes empty. At that point any remaining items in either list are simply moved to the end of the merged list. Note that one of the last two Repeat until parts of the algorithm will not have any effect on the lists, since one of the sorted sub-lists will be empty at this stage. The other 'Repeat until part will move the remaining items in the other sorted sub-list to the sorted list, completing the merge. Create a merge_lists custom block to implement this algorithm. Take a screenshot of your custom block definition script and paste it into your solution document. (12 marks) b. Drag a merge_lists custom block from the More Blocks palette to the scripts area and add it as the last block in the when[s]key_pressed script as shown in Figure 5. when s key pressed delete all of sub_list_1 delete ally of sub_list_2 delete ally of sorted_sub_list_1 delete all of sorted_sub_list_2 delete ally of sorted_list set comparisons to o split_list sort_sublists You should see that unsorted_list is now populated with 20 items. Run your when[s]key_pressed script and note the total number of comparisons required. Repeat the process but this time import list_30.txt, which contains 30 items, and again note the total number of comparisons required. Do the same for list_40.txt which contains 40 items. (list_10.txt contains the original 10 items, should you need them.) Then copy and complete the following table. Number of items 10 20 30 40 Number of comparisons required by selection sort 45 190 435 780 Number of comparisons required by the teacher's new sorting strategy (2 marks) iii. Based on your results comment briefly on how the teacher's new sorting strategy compares with selection sort in terms of the number of comparisons required. (2 marks) iv. Do your results indicate that the relationship between the length of the list and the number of comparisons required by the teacher's new sorting strategy is linear or non-linear? Briefly explain your answer. (2 marks) c. The teacher now has an idea to improve her sorting strategy still further. Suppose instead of splitting the unsorted list into two sub-lists we split it into four. We would sort each sub-list separately and then merge them in two stages, as shown in Figure 6, where we have assumed there are 40 items in the unsorted list. Sub-list 10 items Sorted sub-list 10 items Merge Sorted sub-list 20 items Sub-list 10 items Sorted sub-list 10 items Merge Sorted list 40 items Sub-list 10 items Sorted sub-list 10 items Merge Sorted sub-list 20 items Sub-list 10 items Sorted sub-list 10 items Figure 6 In this part you will work out the largest possible number of comparisons required to sort a list of 40 items using this idea, so the teacher can compare it with the performance of her previous sorting strategy and see if it is more efficient, as she hopes. i. If two sorted sub-lists each of length 10 are merged, using the merge algorithm you used in part (b) above, the largest number of comparisons that will be required is 19. Similarly merging two sub-lists of length 20 requires at most 39 comparisons. Suggest a reason for this. (2 marks) ii. On the basis of the information in part (c) (i) above, and using the fact that sorting a list of 10 items using selection sort requires 10 x (10 - 1)/2 = 45 comparisons as you saw earlier, answer the following questions: How many comparisons will selection sort require to sort 4 lists each of length 10? o What is the maximum number of comparisons required for the two-stage merge process shown in Figure 6? What is the maximum possible number of comparisons that will therefore be required overall using the teacher's new idea to sort a list of 40 items? How does this compare with the number you found for the teacher's sorting strategy in part (b)(ii)? (4 marks) when s key pressed delete all of sub_list_1 delete all of sub_list_2 delete ally of sorted_sub_list_1 delete all of sorted_sub_list_2 delete ally of sorted_list set comparisons to o define split_list delete all of sub_list_1 delete all of sub_list_2 set current_pos to 1 set size to length of unsorted_list repeat until current_pos> size 1 2 to sub_list_1 add item current_pos of unsorted_list change current_pos by 1 repeat until current_pos size to sub_list_2 add item current_pos of unsorted_list change current_pos by 1 define sort_sublists X: -51 y: 76 delete all of sorted_sub_list_1 repeat length of sub_list_1 set current_pos to 2 set min_pos to 1 set min to item min_pos of sub_list_1 repeat until current_pos > length of sub_list_1 change comparisons by 1 if item current_pos of sub_list_1 length of sub_list_2 change comparisons by 1 if item current_pos of sub_list_2 size 1 2 to sub_list_1 add item current_pos of unsorted_list change current_pos by 1 repeat until current_pos size to sub_list_2 add item current_pos of unsorted_list change current_pos by 1 define sort_sublists X: -51 y: 76 delete all of sorted_sub_list_1 repeat length of sub_list_1 set current_pos to 2 set min_pos to 1 set min to item min_pos of sub_list_1 repeat until current_pos > length of sub_list_1 change comparisons by 1 if item current_pos of sub_list_1 length of sub_list_2 change comparisons by 1 if item current_pos of sub_list_2