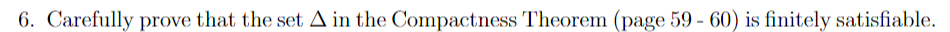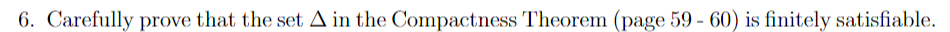
here is the compactness theorem:


6. Carefully prove that the set in the Compactness Theorem (page 5960 ) is finitely satisfiable. COMPACTNESS THEOREM A set of wffs is satisfiable iff every finite subset is satisfiable. Let us temporarily say that is finitely satisfiable iff every finite subset of is satisfiable. Then the compactness theorem asserts that this notion coincides with satisfiability. Notice that if is satisfiable, then automatically it is finitely satisfiable. Also if is finite, then the converse is trivial. (Every set is a subset of itself.) The nontrivial part is to show that if an infinite set is finitely satisfiable, then it is satisfiable. PROOF OF THE COMPACtNESS THEOREM. The proof consists of two distinct parts. In the first part we take our given finitely satisfiable set and extend it to a maximal such set . In the second part we utilize to make a truth assignment that satisfies . For the first part let 1,2, be a fixed enumeration of the wffs. (This is possible since the set of sentence symbols, and hence the set of expressions, is countable; see Theorem 0B.) Define by recursion (on the natural numbers) 0n+1=,={n;n+1n;n+1ifthisisfinitelysatisfiableotherwise. (Recall that n;n+1=n{n+1}.) Then each n is finitely satisfiable; see Exercise 1 . Let =nn, the limit of the n 's. It is clear that (1) and that (2) for any wff either or (). Furthermore, (3) is finitely satisfiable. For any finite subset is already a finite subset of some n and hence is satisfiable. This concludes the first part of the proof; we now have a set having properties (1)-(3). There is in general not a unique such set, but there is at least one. (An alternative proof of the existence of such a and one that we can use even if there are uncountably many sentence symbols - employs Zorn's lemma. The reader familiar with uses of Zorn's lemma should perceive its applicability here.) For the second part of the proof we define a truth assignment v for the set of all sentence symbols: v(A)=TiffA for any sentence symbol A. Then for any wff , we claim that vsatisfiesiff. This is proved by induction on ; see Exercise 2. Since , v must then satisfy every member of . 6. Carefully prove that the set in the Compactness Theorem (page 5960 ) is finitely satisfiable. COMPACTNESS THEOREM A set of wffs is satisfiable iff every finite subset is satisfiable. Let us temporarily say that is finitely satisfiable iff every finite subset of is satisfiable. Then the compactness theorem asserts that this notion coincides with satisfiability. Notice that if is satisfiable, then automatically it is finitely satisfiable. Also if is finite, then the converse is trivial. (Every set is a subset of itself.) The nontrivial part is to show that if an infinite set is finitely satisfiable, then it is satisfiable. PROOF OF THE COMPACtNESS THEOREM. The proof consists of two distinct parts. In the first part we take our given finitely satisfiable set and extend it to a maximal such set . In the second part we utilize to make a truth assignment that satisfies . For the first part let 1,2, be a fixed enumeration of the wffs. (This is possible since the set of sentence symbols, and hence the set of expressions, is countable; see Theorem 0B.) Define by recursion (on the natural numbers) 0n+1=,={n;n+1n;n+1ifthisisfinitelysatisfiableotherwise. (Recall that n;n+1=n{n+1}.) Then each n is finitely satisfiable; see Exercise 1 . Let =nn, the limit of the n 's. It is clear that (1) and that (2) for any wff either or (). Furthermore, (3) is finitely satisfiable. For any finite subset is already a finite subset of some n and hence is satisfiable. This concludes the first part of the proof; we now have a set having properties (1)-(3). There is in general not a unique such set, but there is at least one. (An alternative proof of the existence of such a and one that we can use even if there are uncountably many sentence symbols - employs Zorn's lemma. The reader familiar with uses of Zorn's lemma should perceive its applicability here.) For the second part of the proof we define a truth assignment v for the set of all sentence symbols: v(A)=TiffA for any sentence symbol A. Then for any wff , we claim that vsatisfiesiff. This is proved by induction on ; see Exercise 2. Since , v must then satisfy every member of