Hi, could I get help with the following questions, data and graphs are part of the last two attachments. Thanks!
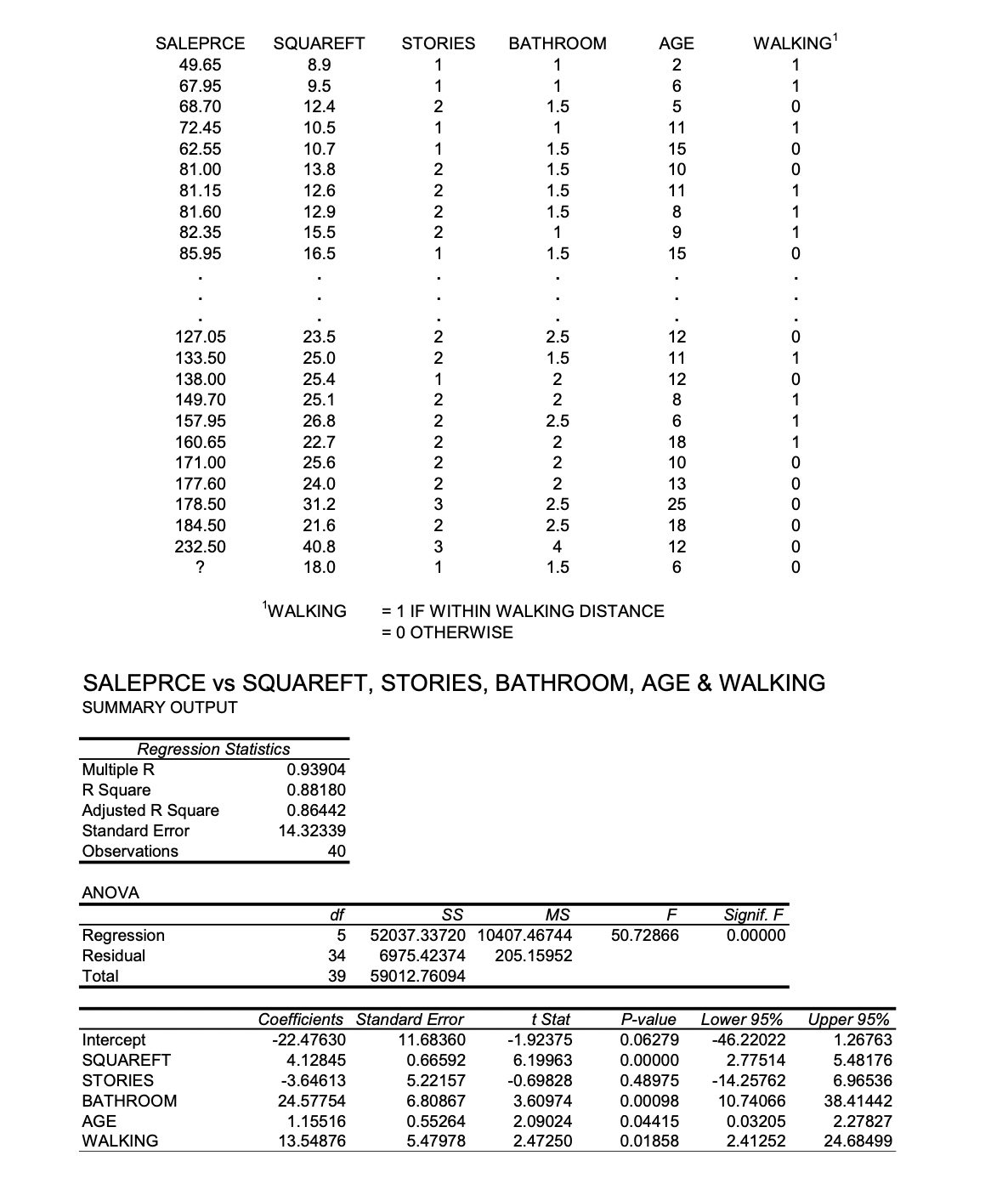
MBATOO HOMEWORK 4 Part I: FOREST SWAMP "It Mget any better than this," thought Rick Blackbird as he took another sip of Molson's Golden Ale and watched the sun set through the mangroves on his estate in Forest Swamp. He had built his 1.800-square-foot, one-story, 1.5-bath mansion six years earlier and was convinced it was the best, if not the most handsome. of the investments he had made. It was true that the gators in the swamp had recently dined on his dog. but this was a minor inconvenience. Besides, he had recently switched to cats. His position at Piedmont Business School was secure due to his best-selling organizational behavior texts. Now that he had decided to permanently settle in the community, he was trying to decide whether to move to a larger (and more appropriate) dwelling, to renovate his existing structure and then sell it, or to stay put and enjoy Forest Swamp. Naturally, he needed to learn more about housing values to make an informed decision. Rick realized he needed some way of determining the values of the houses in his community and. in particular, the value of his own house. Although he could always pay a realtor to do an appraisal, Rick was convinced they frequently overvalued houses in the hope of later obtaining the right to the listing. Because he possessed a keen analytical mind, Rick saw that he was better off trying to develop a statistical model of housing values. A colleague of his, Alan Freebee, mentioned that the problem looked like a natural application of regression analysis. Armed with this idea, Rick went to the county tax ofce and recorded the relevant data from 40 randomly chosen, recent house closings in the community. He gured that the data measured the hard truth, rather than some realtor's hopeful guess as to what a house might sell for. For the 40 closings. Rick recorded the sales price (in $10003). the number of square feet in the house (in 1003 of square feet), the number of stories, the number of bathrooms. the age of the house, and whether the house was in walking distance of the Piedmont campus. Though he and his lovely wife. Jill, personally preferred to live in Forest Swamp (a short drive from campus), he realized that many people were willing to pay a premium to live closer. Rick entered the data into Excel and ran a multiple regression of sales price on the ve housing characteristics. The partial listing of the data and the regression output are given below. As Rick casually brushed a copperhead off the printout, he realized he had a number of unanswered questions about the regression. SALEPRCE SQUAREFT STORIES BATHROOM AGE WALKING 49.65 8.9 2 67.95 95 68.70 12.4 72.45 10.5 62.55 10.7 - in 11 15 81.00 13.8 10 81.15 12.6 11 81.60 12.9 82.35 15.5 85.95 16.5 NNNN- O--400-0- 127.05 23.5 133.50 25.0 138.00 25.4 149.70 25.1 157.95 26.8 160.65 22.7 171.00 25.6 177.60 24.0 178.50 31.2 184.50 21.6 232.50 40.8 ? 18.0 -WNWNNNNN -NN . 15 oooooo - - -0-o . . "WALKING = 1 IF WITHIN WALKING DISTANCE = 0 OTHERWISE SALEPRCE vs SQUAREFT, STORIES, BATHROOM, AGE & WALKING SUMMARY OUTPUT Regression Statistics Multiple R 0.93904 R Square 0.88180 Adjusted R Square 0.86442 Standard Error 14.32339 Observations 40 ANOVA df SS MS F Signif. F Regression 5 52037.33720 10407.46744 50.72866 0.00000 Residual 34 6975.42374 205.15952 Total 39 59012.76094 Coefficients Standard Error t Stat P-value Lower 95% Upper 95% Intercept 22.47630 11.68360 -1.92375 0.06279 -46.22022 1.26763 SQUAREFT 4.12845 0.66592 6.19963 0.00000 2.77514 5.48176 STORIES -3.64613 5.22157 -0.69828 0.48975 -14.25762 6.96536 BATHROOM 24.57754 6.80867 3.60974 0.00098 10.74066 38.41442 AGE 1.15516 0.55264 2.09024 0.04415 0.03205 2.27827 WALKING 13.54876 5.47978 2.47250 0.01858 2.41252 24.684991. What is the value of the coefficient of determination? Is this value significantly greater than zero? Test at the 1 percent level. Support your answer. 2. Which of the calculated slope coefficients are significantly different from zero? Test at the 1 percent level. Support your answer. 3. Obtain a point estimate and approximate 99 percent confidence interval for the value of Rick's house. 4. To finance a new mortgage, Rick would have to sell his existing mansion for at least $80,000. What is the probability that he could do so? Show your work. 5. Building costs in Rick's community currently average about $30 per square foot. Can he make any money if he adds a new family room to the side of his house before he ever sells it? Support your answer.Rick plans to convert his cats' bedroom into a full bathroom. Estimate the change in the selling price of the house if he proceeds with the conversion. Provide a point estimate and a 95 percent condence interval for the change in price. Rick has been told that, other factors being equal, a house that is older (than another house) should be less valuable (due to normal wear and tear). Does the regression provide convincing evidence to refute this theory? Test at the 1 percent level. Show all relevant calculations. draw a picture, and explain how you reached your conclusion. Give your conclusion in terms of the statement of the problem. What is the prob-value for the test? Rick has been looking at a pretty house within walking distance of campus. Unfortunately, the owner of the house has been asking a price that seems unusually high and has been arguing that homebuyers in the Piedmont community are willing to pay at least $20,000 extra to live within walking distance of campus. Does the regression provide convincing evidence to refute the owner's argument? Test at the 1 percent level. Show all relevant calculations, draw a picture, and explain how you reached your conclusion. Give your conclusion in terms of the statement of the problem. What is the prob-value for the test