Hi would it be possible please for someone to adapt my  multi objective genetic code in matlab in order to minimize and maximize the functions and equations established here with these constraints in order to appear an  3D Pareto front ? Do not worry about these values as they are simply for testing.
The project is called optimization of a turbojet afterburner two spool engine

My code unfortunatelly is only for 2D yet.

Thank you so much, I've been stuck here for a long time

The idea is to see in 3D Pareto front maximizing and minimizing the functions in relation to the constraints and to opt for the best overall design.

If it is also possible to establish realistic values for the variables and equations I would be very grateful.

%variables and random values

f=1; % f= fuel to air ratio

Fn=2; % Fn= net thurst

m0=3; % m0= air mass flow rate

p3=4; % p3=inlet pressure

Tpz=5; % Tpz=primary zone temperature

o=6; % o=equivalence ratio

t=7; % t=residence time

aa=8; % aa=pressure term

WTO=9; % Wto=take off weight

WLanding=10; % Wlanding=landing weight

WF=11; % Wf=fuel weight

WE=12; % WE=empty weight

WPL=13; % Wpl=payload weight

WC=14; % Wc=crew weight

M=15; % Fuel load mass

Fab=16; % afterburner fuel-to-air ratio

V9=17; % exhaust velocity

V0=18; % cruising speed

f=19; % fuel to air ratio

QR=20; % fuel heating value

NB=21; % burner efficiency

T1=22; % inlet temperature

T0=23; % ambient static temperature

L=24; % lift

p=25; % density

V=26; % velocity

A=27; % wing area

bw=28; % wing span

sw=29; % Trapezoidal wing area in ft

WZF=30; % zero fuel weight

b=31; % upper dimension of wing

cr=32; % right dimension side of wing

ct=33; % left dimension side of wing

WS=34; % wing span

RC=35; % root chord

l=36; % lenght

m=37; % moment

W0=38; % gross weight of aicraft

VH=39; % maximum demonstrated level airpeed

VS=40; % stalling speed

VS1=41; % stalling speed with flaps retracted

KG=42; % Gust alleviation factor

UREF=43; % reference gust velocity

VC=44; % design cruise speed

pi=3.14; % pi number

Ude=45; % vertical gust velocity

x=46; % distance in ft penetrated into the gust

CMGC=47; % Mean geometric chord

UG=48; % i dont know the name

D=49; % Drag

Y=Wi/Wf; % fuel weight fraction for the cruise segment

Y1=49;

CL=51; % lift coefficient

CD=52; % drag coefficient

A=53; % Area

Cla=54; %3-dimensional lift curve slope

B=log(Y);

%Maximize this functions :

NP=((Fn/m0)*V0)/(1+f+Fab)*((V9^2)/2)-((V0^2)/2); % propulsive efficiency

NO=((Fn/m0)*V0)/(f*QR*NB); % overall efficiency

TE=1-(1/(T1/T0)); % thermal efficiency

T=m0*V0; % Thurst

% while Minimize this ones :

TSFC =(f/(Fn/m0)); % TSFC=specific fuel consumption

Nox=(10^13)*(p3/(1.4*(10^6)))*exp(-71442/Tpz)*(7.56*(o^7.2)-1.6)*(t^0.64); % NOx Emissions (LTO)

WF=WTO-WLanding; % Fuel Weight

WTO=WT0*(1-(WF/WTO)-(WE/WTO)); % take off weight

WTO=WPL/WC; % take off weight

maxFT=M/(TSFC/Fn); % max flight time

% under all this constraints

CLmin=L/(p*(V^2)*(A/2)); % minimum lift coefficient -must be equal or less than 2

CLmax=L/(p*(V^2)*(A/2)); % maximum lift coefficient-must be equal or less than 2

WW=(17*bw*sw*sqrt(WZF/WTO)); % wing weight-must be equal or less than 2

S=b*((cr+ct)/2); % wing planform area -must be equal or less than 2

WV=(5*WS*RC*l)/0.5; % wing volume-must be equal or less than 2

PM=m/(0.5*p*V^2)*(A^2); % Pitching moment-must be equal or less than 2

LF=2.1+(24000/(W0+10000)); % Load factor -must be equal or less than 2

MaximumDCS=(33*sqrt((W0)/S)); % minimum design cruising speed-must be equal or less than 2

MinimumDCS=0.9*VH; % maximum design cruising speed-must bigger or equal than 2

DDS=VD>1.4*MinimumDCS; % design dive speed-must bigger or equal than 2

nplus=(0.003388*(V^2)*S*CLmax)/W0; % Positive stall line-must bigger or equal than 2

nless=(-0.003388*(V^2)*S*CLmin)/W0; % Negative stall line-must bigger or equal than 2

VA=VS*sqrt(nplus); % maneuvering speeds -must bigger or equal than 2

VG=sqrt((2*nless*W)/(p*S*CLmin)); % maneuvering speeds -must bigger or equal than 2

DSMGI=VS1*((KG*UREF*VC*a)/498*W0)^1/3; % Design speed for maximum Gust Intensity-must be between 2 and 4

GLF=1+((KG*Ude*V*Cla)/(498*(W0/WS))); % Gust load factor-must be between 2 and 4

GAF=0.88*UG/(5.3+UG); % Gust alleviation factor -must be between 2 and 4

R=(V/TSFC)*(L/D)*ln(Wi/WF); % Range-must be between 2 and 4

E=((1/TSFC)*(CL/CD)*B); % Endurance -must be between 2 and 4

M=p*A*V; % mass flow rate-must be between 2 and 4

Its possible please to convert this to matlab code in order to work and plot a 3D Pareto front with all this information please ?

NOTE:This is a personal project not an assignement 

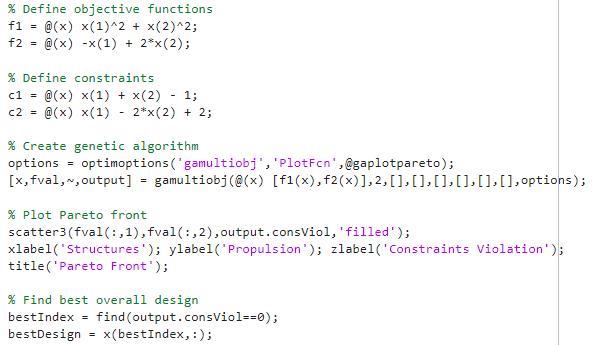
Image transcription text

% Define objective functions f1 = @(x) x(1)^2 + x(2)^2; f2 = @(x) -x(1) + 2*x(2) ; Define constraints c1 = @(x) x(1) + x(2) - 1; c2 = @(x) x(1) - 2*x(2)
+ 2; % Create genetic algorithm options = optimoptions('gamultiobj ' , 'PlotFen" ,@gaplotpareto) ; [x, fval,~, output] = gamultiobj(@(x) [f1(x) ,
f2(*)],2,,,,,,,options); Plot Pareto front scatter3(fval(:,1) , fval(:, 2) , output. consViol, 'filled'); xlabel( 'Structures'); ylabel( ' Propulsion' ); ... 

 
 

% Define objective functions f1 = @(x) x(1)^2 + x(2)^2; f2= @(x)x(1) +2*x(2); % Define constraints c1 = @(x) x(1) + x(2) - 13 c2= @(x) x(1) 2*x(2) + 2; - % Create genetic algorithm options = optimoptions('gamultiobj', 'PlotFcn', @gaplotpareto); [x, fval,~, output] = gamultiobj (@(x) [f1(x), f2(x)], 2, [], [], [], [], [], [], options); % Plot Pareto front scatter3 (fval(:,1), fval(:,2), output. consViol, 'filled'); xlabel('Structures'); ylabel('Propulsion'); zlabel('Constraints Violation'); title('Pareto Front'); % Find best overall design bestIndex = find(output.consViol==0); bestDesign = x(bestIndex,);