how do i use the calculation in photo 1 to solve the problems in photo 2

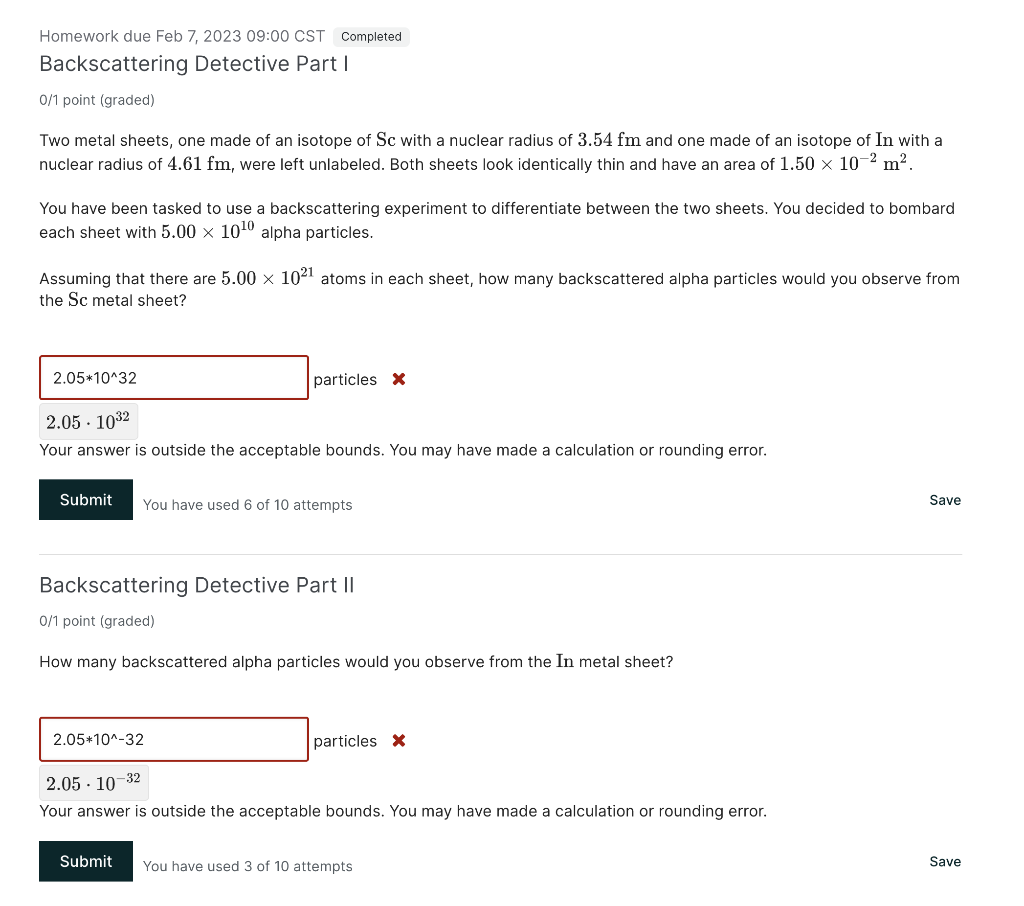
You decide to perform your own backscattering experiment with the help of your classmates. Your setup consists of a regular lattice of area 1.00m2, which has 125 spheres of unknown radius evenly distributed throughout the lattice. Together, the class bombards the setup with exactly 200 ping-pong balls and you record a total of 29 backscattered pingpong balls. Using these data, calculate the radius (in m ) of each sphere in the lattice. m Answer: 0.0192 0.0192 Correct. Explanation The fraction of the area of the lattice occupied by cross-sectional area of the spheres is equivalent to the probability of hitting a sphere with a ball: TotalLatticeAreaTotalSphereArea=TotalNumberofTrialsNumberofHits1.00m2125AreaofaSphere=20029=0.1450 From this, we can solve for the cross-sectional area of one sphere: AreaofaSphere=1250.14501.00m2=0.001160m2 The formula relating cross-sectional area to the radius is the formula of the area of a circle: Area=r2 The radius of an individual sphere can be calculated after rearranging the equation: r=Area=0.001160=0.0192m 0/1 point (graded) Two metal sheets, one made of an isotope of Sc with a nuclear radius of 3.54fm and one made of an isotope of In with a nuclear radius of 4.61fm, were left unlabeled. Both sheets look identically thin and have an area of 1.50102m2. You have been tasked to use a backscattering experiment to differentiate between the two sheets. You decided to bombard each sheet with 5.001010 alpha particles. Assuming that there are 5.001021 atoms in each sheet, how many backscattered alpha particles would you observe from the Sc metal sheet? particles x 2.051032 Your answer is outside the acceptable bounds. You may have made a calculation or rounding error. You decide to perform your own backscattering experiment with the help of your classmates. Your setup consists of a regular lattice of area 1.00m2, which has 125 spheres of unknown radius evenly distributed throughout the lattice. Together, the class bombards the setup with exactly 200 ping-pong balls and you record a total of 29 backscattered pingpong balls. Using these data, calculate the radius (in m ) of each sphere in the lattice. m Answer: 0.0192 0.0192 Correct. Explanation The fraction of the area of the lattice occupied by cross-sectional area of the spheres is equivalent to the probability of hitting a sphere with a ball: TotalLatticeAreaTotalSphereArea=TotalNumberofTrialsNumberofHits1.00m2125AreaofaSphere=20029=0.1450 From this, we can solve for the cross-sectional area of one sphere: AreaofaSphere=1250.14501.00m2=0.001160m2 The formula relating cross-sectional area to the radius is the formula of the area of a circle: Area=r2 The radius of an individual sphere can be calculated after rearranging the equation: r=Area=0.001160=0.0192m 0/1 point (graded) Two metal sheets, one made of an isotope of Sc with a nuclear radius of 3.54fm and one made of an isotope of In with a nuclear radius of 4.61fm, were left unlabeled. Both sheets look identically thin and have an area of 1.50102m2. You have been tasked to use a backscattering experiment to differentiate between the two sheets. You decided to bombard each sheet with 5.001010 alpha particles. Assuming that there are 5.001021 atoms in each sheet, how many backscattered alpha particles would you observe from the Sc metal sheet? particles x 2.051032 Your answer is outside the acceptable bounds. You may have made a calculation or rounding error