How would the price of the bond be affected by a change in the going market interest rate? (Hint: Conduct a sensitivity analysis of price to changes in the going market interest rate for the bond. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. This is an oversimplification, but assume it for purposes of this problem.) Round your answers to the nearest cent.
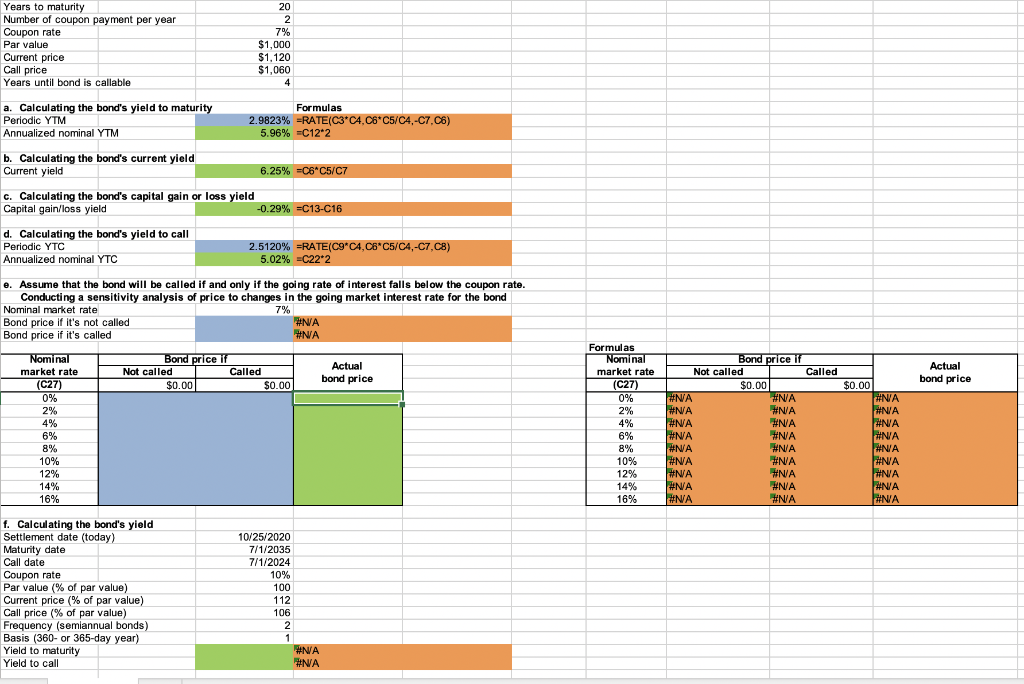
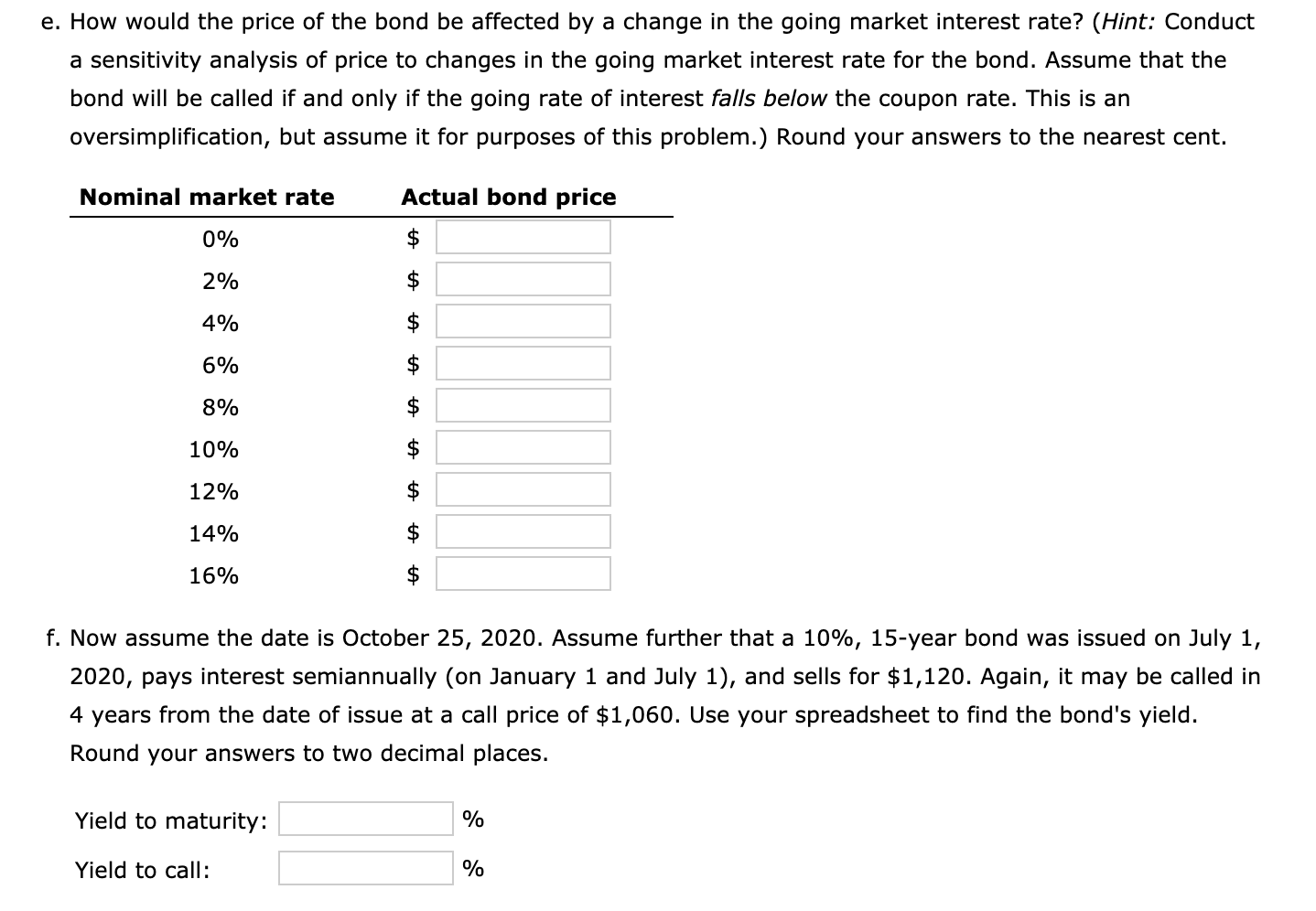
Years to maturity Number of coupon payment per year Coupon rate Par value Current price Call price Years until bond is callable 20 2 7% $1,000 $1,120 $1,060 4 a. Calculating the bond's yield to maturity Periodic YTM Annualized nominal YTM Formulas 2.9823% =RATE(C3 C4,C6*C5/C4,-C7.C) 5.96% =C122 b. Calculating the bond's current yield Current yield 6.25% =C6 C5/C7 c. Calculating the bond's capital gain or loss yield Capital gain/loss yield -0.29% C13-C16 d. Calculating the bond's yield to call Periodic YTC 2.5120% =RATE(C9*CA,C6 C5/C4,-C7,C8) Annualized nominal YTC 5.02% =C222 Actual bond price e. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. Conducting a sensitivity analysis of price to changes in the going market interest rate for the bond Nominal market rate 7% Bond price if it's not called #NA Bond price if it's called #NA Nominal Bond price if market rate Not called Actual Called (C27) $0.00 bond price $0.00 0% % 2% 4% 6% % 8% 10% 12% 14% 16% Formulas Nominal market rate (C27) 0% 2% 4% 6% 8% 10% 12% 14% 16% Bond price if Not called Called $0.00 $0.00 #NA #NA #N/A #NA #N/A #N/A #NA #NA #N/A #N/A #NA #NA #N/A #NA #NA #N/A #NA #NA #NA WNA #NA #NA #N/A N #NA #N/A #N/A #NA #NA #N/A f. Calculating the bond's yield Settlement date (today) Maturity date Call date Coupon rate Par value (% of par value) Current price (% of par value) Call price% of par value) Frequency (semiannual bonds) Basis (360- or 365-day year) Yield to maturity Yield to call 10/25/2020 7/1/2035 7/1/2024 10% 100 112 106 2 1 #NA #NA e. How would the price of the bond be affected by a change in the going market interest rate? (Hint: Conduct a sensitivity analysis of price to changes in the going market interest rate for the bond. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. This is an oversimplification, but assume for purposes of this problem.) Round your answers to the nearest cent. Nominal market rate Actual bond price 0% $ 2% 4% 6% 8% $ 10% 12% $ 14% 16% $ f. Now assume the date is October 25, 2020. Assume further that a 10%, 15-year bond was issued on July 1, 2020, pays interest semiannually (on January 1 and July 1), and sells for $1,120. Again, it may be called in 4 years from the date of issue at a call price of $1,060. Use your spreadsheet to find the bond's yield. Round your answers to two decimal places. Yield to maturity: % Yield to call: % Years to maturity Number of coupon payment per year Coupon rate Par value Current price Call price Years until bond is callable 20 2 7% $1,000 $1,120 $1,060 4 a. Calculating the bond's yield to maturity Periodic YTM Annualized nominal YTM Formulas 2.9823% =RATE(C3 C4,C6*C5/C4,-C7.C) 5.96% =C122 b. Calculating the bond's current yield Current yield 6.25% =C6 C5/C7 c. Calculating the bond's capital gain or loss yield Capital gain/loss yield -0.29% C13-C16 d. Calculating the bond's yield to call Periodic YTC 2.5120% =RATE(C9*CA,C6 C5/C4,-C7,C8) Annualized nominal YTC 5.02% =C222 Actual bond price e. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. Conducting a sensitivity analysis of price to changes in the going market interest rate for the bond Nominal market rate 7% Bond price if it's not called #NA Bond price if it's called #NA Nominal Bond price if market rate Not called Actual Called (C27) $0.00 bond price $0.00 0% % 2% 4% 6% % 8% 10% 12% 14% 16% Formulas Nominal market rate (C27) 0% 2% 4% 6% 8% 10% 12% 14% 16% Bond price if Not called Called $0.00 $0.00 #NA #NA #N/A #NA #N/A #N/A #NA #NA #N/A #N/A #NA #NA #N/A #NA #NA #N/A #NA #NA #NA WNA #NA #NA #N/A N #NA #N/A #N/A #NA #NA #N/A f. Calculating the bond's yield Settlement date (today) Maturity date Call date Coupon rate Par value (% of par value) Current price (% of par value) Call price% of par value) Frequency (semiannual bonds) Basis (360- or 365-day year) Yield to maturity Yield to call 10/25/2020 7/1/2035 7/1/2024 10% 100 112 106 2 1 #NA #NA e. How would the price of the bond be affected by a change in the going market interest rate? (Hint: Conduct a sensitivity analysis of price to changes in the going market interest rate for the bond. Assume that the bond will be called if and only if the going rate of interest falls below the coupon rate. This is an oversimplification, but assume for purposes of this problem.) Round your answers to the nearest cent. Nominal market rate Actual bond price 0% $ 2% 4% 6% 8% $ 10% 12% $ 14% 16% $ f. Now assume the date is October 25, 2020. Assume further that a 10%, 15-year bond was issued on July 1, 2020, pays interest semiannually (on January 1 and July 1), and sells for $1,120. Again, it may be called in 4 years from the date of issue at a call price of $1,060. Use your spreadsheet to find the bond's yield. Round your answers to two decimal places. Yield to maturity: % Yield to call: %








