I am trying to use Principal Component Analysis Regression (PCA-R) to fit data, and then determine uncertainty using SEP - Standard error of prediction. I then want to predict the concentrations of the unknown sample (Au).

But I keep getting this error with varying numbers. First it said 1 is different from 2 then 1 is different from 12 then 12 is different from 200 and now 11 is different from 12.

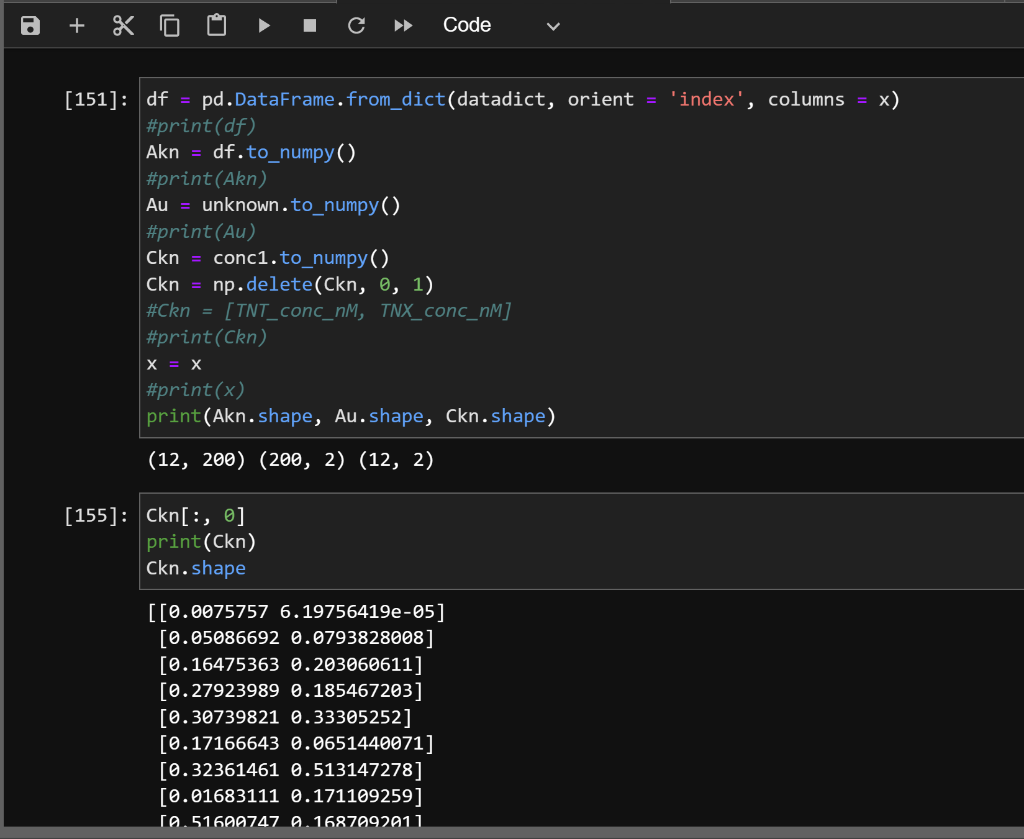
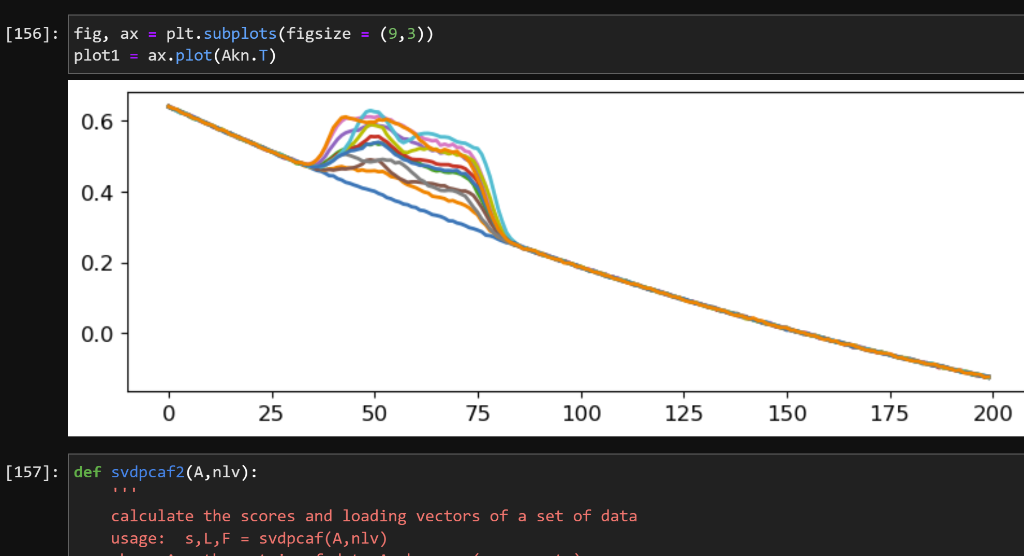
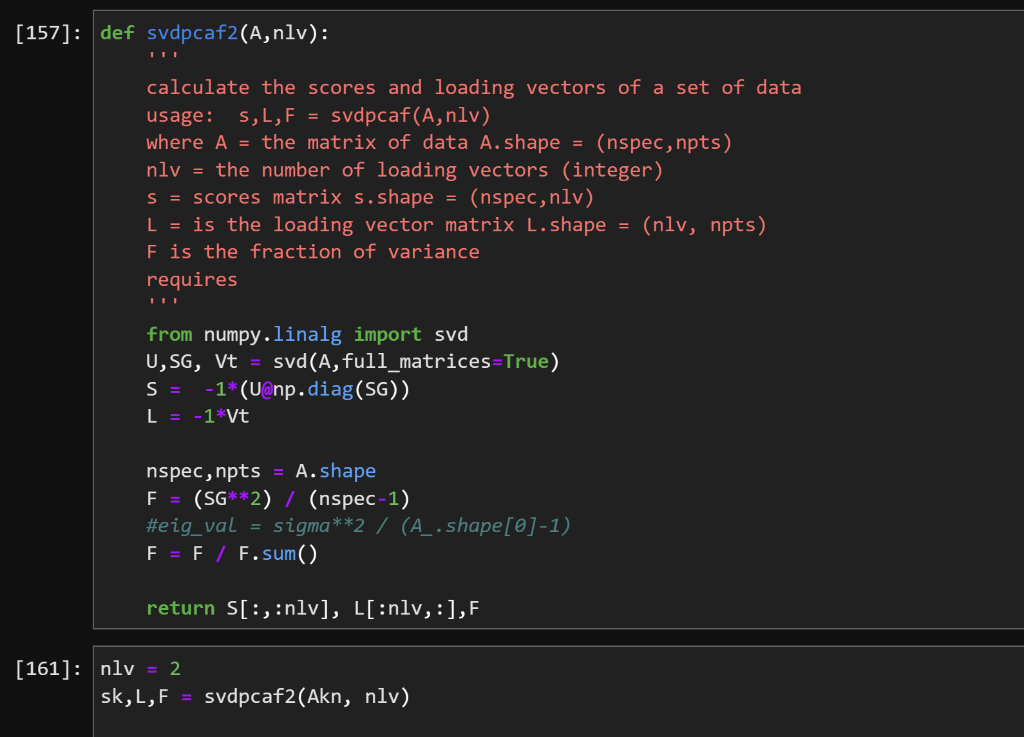
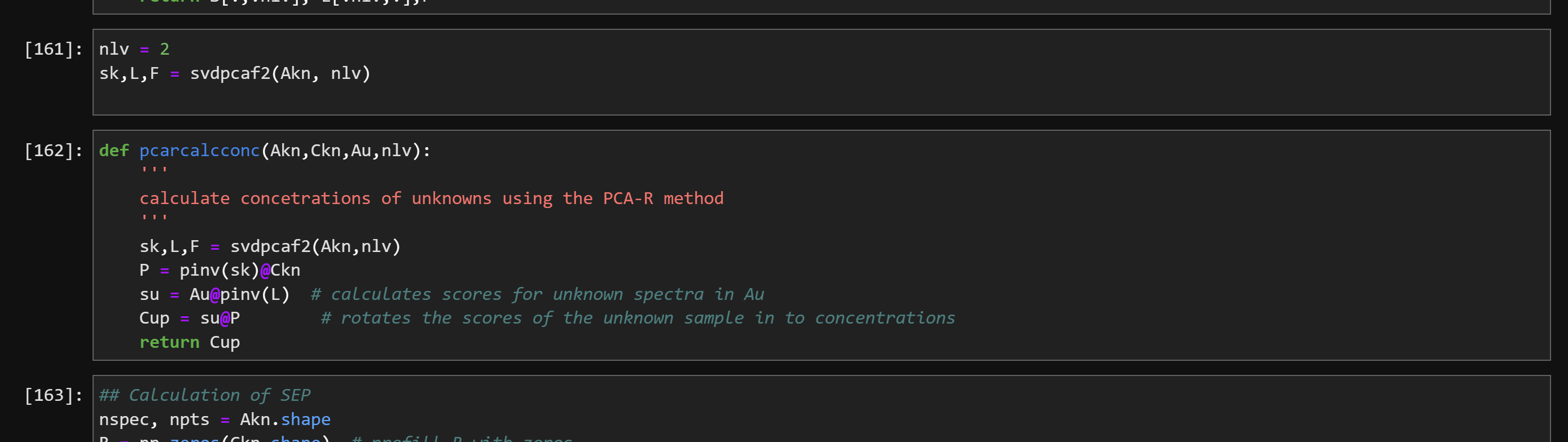
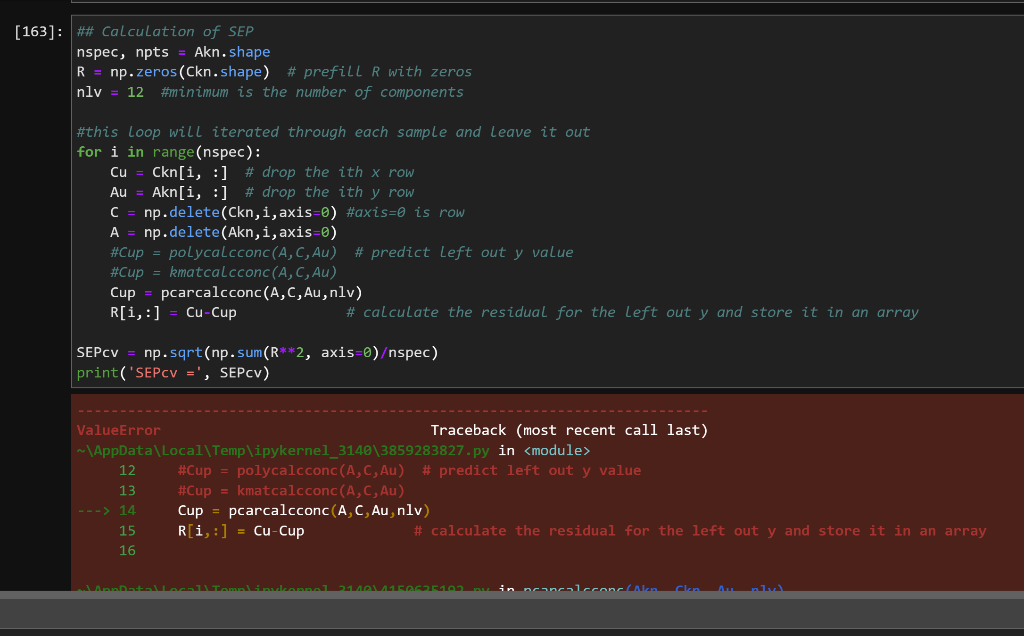
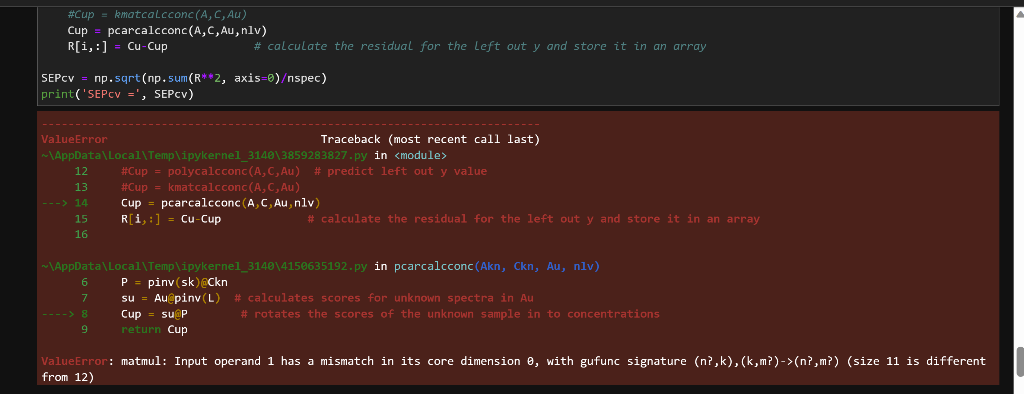
df= pd.DataFrame. from_dict(datadict, orient = 'index', columns =x ) \#print (df) Akn=df.to_numpy () \#print(Akn) Au= unknown.to_numpy () \#print(Au) Ckn = conc1.to_numpy () Ckn =npdelete(Ckn,0,1) \#Ckn = [TNT_Conc_nM, TNX_Conc_nM] \#print(Ckn) x=x \#print (x) print(Akn.shape, Au. shape, Ckn.shape) (12,200)(200,2)(12,2) Ckn[20] print (Ckn) Ckn.shape [[0.00757576.19756419e05] [0.050866920.0793828008] [0.164753630.203060611] [0.279239890.185467203] [0.307398210.33305252] [0.171666430.0651440071] [0.323614610.513147278] [0.016831110.171109259] [. 51690747 . 16879)1] fig, ax= plt. subplots (figsize = (9,3)) plot1 = ax.plot (AknT) def svdpcaf2(A,nlv): 1,1 calculate the scores and loading vectors of a set of data usage: s,L,F=svdpcaf(A,nlv) def svdpcaf2( A,nlv) : ' calculate the scores and loading vectors of a set of data usage: s,L,F=svdpcaf(A,nlv) where A= the matrix of data A.shape = (nspec, npts) nlv = the number of loading vectors (integer) s= scores matrix s. shape =( nspec, nlv) L= is the loading vector matrix L. shape = (nlv, npts) F is the fraction of variance requires ' ' from numpy.linalg import svd U,SG, Vt = svd(A,full_matrices=True) S=1(U@npdiag(SG)) L=1Vt nspec, npts = A. shape F=(SG2)/( nspec -1) F=F/Fsum() return S[:,:nlv],L[:nlv,:],F lv=2 nlv=2 sk,L,F=svdpcaf2(Akn,nlv) def pcarcalcconc (Akn,Ckn,Au,nlv): ' ' calculate concetrations of unknowns using the PCA-R method ' ' sk, L,F=svdpcaf2(Akn,nlv) P=pinv(sk)@Ckn su = Au@pinv(L) \# calculates scores for unknown spectra in Au Cup = su@P \# rotates the scores of the unknown sample in to concentrations return Cup \#\# Calculation of SEP nspec, npts = Akn. shape \#\# Calculation of SEP nspec, npts=Akn. shape R=npzeros(Ckn.shape) \# prefilL R with zeros nlv=12 \#minimum is the number of components \#this loop will iterated through each sample and leave it out for i in range(nspec): Cu=Ckn[i,:] \# drop the ith x row Au=Akn[i,:] \# drop the ith y row C=np delete(Ckn, i,axis =) \#axis=0 is row A=npdelete(Akn,i, axis =0) \#Cup = polycalcconc (A,C,Au)# predict left out y value \#Cup = kmatcalcconc (A,C,Au) Cup = pcarcalcconc (A,C,Au,nlv) R[i,:]= Cu-Cup \#calculate the residual for the left out y and store it in an array SEPCV=np.sqrt(npsum(R2,axis=0)spec)print(SEPCV=,SEPCV) ValueError 12 13 14 15 16 \#Cup = polycalcconc (A,C,Au) \# predict left out y value \#Cup = kmatcalcconc (A,C,Au) Cup = pcarcalcconc (A,C,Au,nlv) R[i,:]=CuCup \# calculate the residual for the left out y and store it in an array \#Cup = kmatcalcconc (A,C,Au) Cup = pcarcalconc (A,C,Au,nlv) R[i,:]=Cu-Cup calculate the residual for the left out y and store it in an array SEPcv =np5qt(np+5um(R2, axis =)spec) print ('SEPCV = ', SEPcV) ValueError Traceback (most recent call last) 12 \#Cup = polycalcconc (A,C,Au)# predict left out y value 13 \#Cup = kmatcalcconc (A,C,Au) Cup = pcarcalcconc (A,C,Au,nlv) R[i,i]= Cu-Cup \# calculate the residual for the left out y and store it in an array 15 16 6P=pinv(sk)eCkn su = AuCpinv(L) \# calculates scores for unknown spectra in Au Cup = su@P \# rotates the scores of the unknown sample in to concentrations return Cup ValueError: matmul: Input operand 1 has a mismatch in its core dimension , with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 11 is different from 12)